Перших похідних

Уникнути похибок описання моделі можна шляхом двомірного трасування променів на основі рівняння ейконалу. Але можливий і інший шлях - використання більш простого ніж (9.1) хвильового рівняння, яке дозволяє побудувати просту кінцево-різницеву схему продовження поля вниз, не накладаючи обмежень на геометрію середовища.

Приймемо за основу скалярне (відносно U(х,z,t)) хвильове рівняння

, (9.2)

де - вектор, модуль якого рівний швидкості пружних хвиль в даній точці середовища, а напрям коленіарно променям плоскої хвилі U(х,z,t). Принциповою відмінністю (9.2) від (9.1) є апроксимація хвильового поля суперпозицією плоских а не сферичних (дифрагованих) хвиль. Оскільки операція продовження поля вниз потребує його неперервності, умовою якого є відповідність поля рівнянню Лапласа

(9.3)

покажемо, що поле, яке описано рівнянням (9.2), задовольняє (9.3). Припустимо R=tV, тоді (9.2) запишеться у вигляді:

(9.4)

де - одиничні вектора у напрямку х,z та поширення хвилі. Піддамо (9.4) дії диференціального оператора div(•) та, враховуючи, що rоt rоt скалярного поля рівний 0, отримаємо

Таким чином, поле, яке відповідає рівнянню (9.2), може бути продовжене у нижній півпростір.

Для побудови кінцево-різницевої схеми продовження поля вниз піднесемо (2) у квадрат

(9.5)

Розпишемо вираз (9.5) через кінцеві різниці навколо точки U(х,z,t).

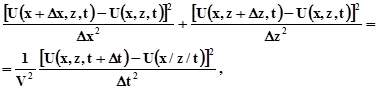
(9.6)

де Dx, Dt - кроки сітки поля U(х,0,t) z - крок, який дорівнює перерахунку поля по глибині.

Однак, рівняння (9.6), вирішене відносно U(х,z+Dz,t) буде давати коректне продовження поля вниз лише при постійності похідних по х і t, оскільки володіє явно вираженою асиметрією. По положенню точок вибору значень поля у площинах x,0,t та z,0,t назвемо таку схему Г-схемою. У випадку міграції реальних хвильових полів слід попіклуватися про симетрію вибірки відносно міграційної точки. Враховуючи, що при продовженні поля на рівень z+Dz час приходу вертикально збіжної хвилі зменшується на величину 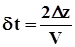і поклавши , що дозволяє проводити міграцію безпосередньо на планшеті завдання вихідного поля, отримаємо

(9.7)

Звідки випливає проста формула міграції поля U(х,z,t)

,

(9.8)

де .

Це Т-схема міграції.

Неважко бачити, що швидкість обчислювального процесу визначається, в основному, затратами часу на вилучення квадратного кореня з виразу (9.8). При міграції планшета NхN буде потрібно N рівней перерахунку, причому середнє число дискретів по t, на одному рівні змінюючись від N-1 до 1, складе N/2. Таким чином, для міграції необхідно виконати N³/2 вилучень квадратного кореня. Відмітимо, що міграція по Кірхгофу потребує N^з таких самих операцій та додаткового поля зображення мігрованого розрізу NхN дискретів. Звідси очевидні переваги запропонованої кінцево-різницевої схеми міграції сейсмічного часового розрізу t₀ на основі рішення хвильового рівняння в часткових похідних першого порядку.

Поиск по сайту: