АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Його дисперсійне співвідношення

Читайте также:
  1. Види інноваційних стратегій та їх співвідношення
  2. Використання логічних операторів та операторів співвідношення
  3. За допомогою рівнянь (V.3.1) і (V.4.5) одержимо співвідношення
  4. Закон в англійській правовій системі. Співвідношення закону і прецеденту
  5. Оптимальне співвідношення ресурсів
  6. Паритет купівельної сили – співвідношення між двома (кількома)
  7. Поняття влади. Співвідношення політичної та державної влади, державної влади і держави
  8. Поняття довжини відрізка та способів його вимірювання. Основні властивості довжини. Одиниці вимірювання довжини та співвідношення між ними.
  9. Поняття площі плоскої фігури, її основні властивості та способи вимірювання. Рівновеликі та рівноскладені фігури. Одиниці вимірювання площі та співвідношення між ними.
  10. Поняття, ознаки і види соціальних норм, їх співвідношення з технічними нормами
  11. Пропускна спроможність та співвідношення сигнал/завада

,

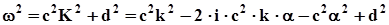(6.5)

знову приводить в силу умови 2 до вимоги a = 0, а вираз (5) спрощується

.

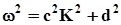для рівняння (6.4) фазова швидкість дорівнює

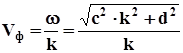, (6.6)

а групова швидкість

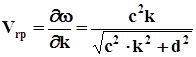. (6.7)

Вирази (6.6) та (6.7) вказують на дисперсію швидкостей, а їх добуток відповідає умові 3.

Отже для рівнянь (6.2) та (6.4) в силу умови 2 коефіцієнт затухання дорівнює 0, оскільки при переході до дисперсійного співвідношення у ньому виявляється лише один уявний член. Якщо хвильове рівняння буде містити дисипативний член, пропорційний похідній поля зміщення, буде спостерігатись затухання хвиль. Причому степінь похідної має бути непарна, якщо у другому члені хвильового рівняння парна похідна по X або парною, якщо другий член містить непарну просторову похідну.

Розглянемо поширення хвиль у середовищі, яке описується наступним хвильовим рівнянням

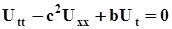. (6.8)

Дисипативний член у рівнянні (6.8) пропорційний швидкості зміщення часток середовища, а поглинання енергії пружних хвиль обумовлено в'язким тертям, наприклад, при перетіканні флюїду у поровому просторі.

Можна показати, що рівняння (6.8) описує тіло Максвела. Дисперсійне співвідношення для (6.8) має вигляд

.

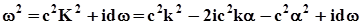(6.9)

Вираз (6.9) в силу умови 2 створює систему рівнянь

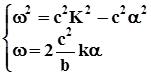. (6.10)

Розв’язуючи (6.10) відносно a, отримаємо

. (6.11)


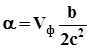1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)