Проаналізуємо четверту модель. Її хвильовому рівнянню

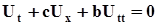(6.27)

відповідає рівняння стану середовища

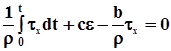. (6.28)

Перетворимо (6.28) аналогічно (6.25) і отримаємо

(6.29)

або

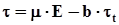(6.29’)

При 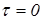з (6.29) маємо

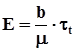, (6.30)

тобто залишкова деформація пропорційна похідній по часу від напруження. Співвідношення (6.30) вказує на те, що площа петлі гістерезіса в момент часу, коли 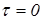, контролюється похідною напруження, оскільки зв’язок деформації з напруженням у цей момент часу неможливий. Із співвідношення (6.30) слідує ще один важливий висновок - коефіцієнт b не може бути постійною величиною. У протилежному випадку величина залишкової деформації при збільшенні може перебільшити величину деформації, яка викликається максимальним напруженням. Оскільки похідна 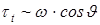, якщо 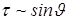, коефіцієнт b повинен бути обернено пропорційним до . З врахуванням цього рівняння (6.27) набуде вигляду

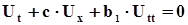, (6.31)

де 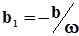. Тут знак мінус вибраний тому, що у виразі (6.30) знак залишкової деформації повинен бути зворотним знаку похідної напруження. Підставляючи замість b у таблиці 6.2, отримаємо для коефіцієнта поглинання

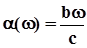. (6.32)

Таким чином, ми отримаємо вираз для , який повністю відповідає експериментальним даним, - коефіцієнт поглинання прямо пропорційний до частоти коливань та обернено пропорційний до швидкості поширення пружних хвиль.

Слід відмітити, що для фізичної реалізації тої чи іншої моделі середовища необхідно виконання критерію Пейлі-Вінера, за яким коефіцієнт поглинання не може бути функцією частоти в усьому діапазоні частот. Отриманий тут коефіцієнт поглинання (6.32) віддзеркалює процес дисипації енергії за рахунок залишкової деформації тіла в процесі поширення пружних хвиль, а коефіцієнт b обернено пропорційний межі текучості матеріалу. Відомо, що ця межа залежить від швидкості деформації. Зменшення пластичних деформацій із зростанням частоти “вимикає” механізм поглинання пружних хвиль за верхньою межею сейсмічного (а, можливо, і акустичного) діапазону. Іншими словами, для задоволення критерію Пейлі-Вінера достатньо припустит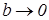и при .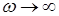

Таким чином, отримане хвильове рівняння (6.31) має мінімальне число параметрів (с і b), містить лише одну другу похідну поля зміщення, добре узгоджується з експериментальними даними та може, по О.К.Кондратьєву, називатись оптимальним хвильовим рівнянням. Перевага (6.31), перш за все, в більш простому вигляді і наявності лише однієї другої похідної. Причому це похідна по часу і її обчислення не складає таких проблем, як других просторових похідних, оскільки крок реальних сейсмічних даних по t більш кореспондує з заміною похідних на кінцеві різниці, ніж крок по x. Отже, запропоноване хвильове рівняння (6.31) є кращою основою для побудови кінцево-різницевих схем міграції даних сейсморозвідки для реальних (поглинаючих) середовищ.

Поиск по сайту: