Узагальнений закон Гука

Встановимо зв’язок між компонентами напружень і деформації.

Виділимо в пружному тілі елементарний об’єм у вигляді призматичного стержня з ребрами, паралельними трьом головним вісям напружень 1, 2, 3, і центром в точці 0 (рисунок 3.1). Тоді перпендикулярно до граней стержня, тобто вздовж осей 1, 2, 3, будуть діяти головні напруження , , 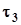. Вони будуть зміщувати точки пружного тіла, що лежать на осях 1, 2, 3, вздовж цих осей. Таким чином, осі 1, 2, 3 будуть і головними осями деформації.

Будемо вважати, що деформації стержня малі. В цьому випадку на основі закону Гука можна стверджувати, що деформації його будуть прямо пропорційні напруженням.

Знайдемо видовження стержня вздовж осі 1. Під дією тільки сили це видовження, згідно (3.1), буде

, (3.3)

де 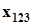- довжина стержня вздовж осі 1 до прикладення сил; - модуль Юнга пружного тіла.

Рисунок 3.1 – Деформація стержня під дією напружень

Одночасно з силою вздовж осі 2 діє сила . Ця сила вздовж осі 1 призводить поперечне стиснення , яке можна знайти на основі (3.2):

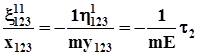, (3.4)

де - число Пуассона; - довжина стержня вздовж осі 2 до прикладення сил; - видовження стержня вздовж осі 1.

Поперечне стиснення 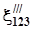, під дією сили 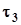визначається із співвідношення

. (3.5)

Загальне видовження під дією всіх трьох сил , , 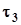на основі (3.3), (3.4) і (3.5) буде

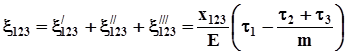
або з врахуванням (1.20)

(3.6)

Аналогічно, розглядаючи загальне подовження вздовж вісей 2 і 3, отримаємо

(3.7)

(3.8)

Позначимо . Тоді вирази (3.6), (3.7) і (3.8) можна записати інакше

(3.9)

Замість модуля Юнга Е та числа Пуасона m часто розглядають, так звані, коефіцієнти Ламе l і m. Вони також характеризують пружні властивості ізотропних тіл.

Просумуємо рівняння системи (3.9). Враховуючи, що

будемо мати

Звідси

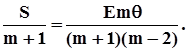
Позначимо

(3.10)

(3.11)

З врахуванням (3.10) і (3.11) система (3.9) буде

(3.12)

Перейдемо тепер від системи координат 1, 2, 3 до довільної системи x, y, z. Через a, b, g позначимо, спрямовуючи косинуси осей х, y, z в системі 1, 2, 3. Помножимо перше рівняння (3.12) на 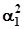, друге на , трете на та складемо їх. Тоді на підставі (1.28) і (2.23) отримаємо

(3.13)

Помножимо ті самі рівняння систем (3.12) на , , 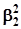, а потім - відповідно на , , . Після додавання на підставі сумування квадратів спрямовуючих косинусів отримаємо

(3.14)

(3.15)

Далі, помножимо перше рівняння (3.12) на , друге на 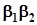, трете на 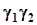. Після складання отримаємо

(3.16)

Помножимо те саме рівняння (3.12) на ,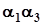
, , а потім їх же на , , 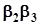. Додаючи, в обох випадках, отримаємо

(3.17)

. (3.18)

Розв’яжемо тепер рівняння (3.13), (3.14), (3.15), (3.16), (3.17) і (3.18) відносно компонент напруження. Отримаємо

(3.19)

Формули (3.19) – це узагальнений закон Гука. Беручи до уваги, що

;

;

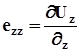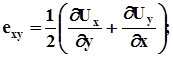
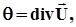
Остаточно маємо наступні залежності між компонентами векторів напруження і складовими векторами зміщень:

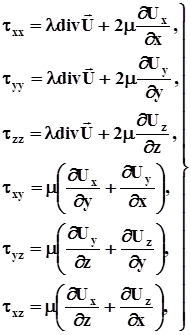(3.20)

Це модифікація узагальненого закону Гука в переміщення. Фізичний зміст перших трьох формул полягає у тому, що кожне нормальне напруження характеризує в основному лінійну деформацію в тому ж напрямку. Тому в ці вирази входять деформації Ці деформації будуть супроводжуватися поперечним стиском або розтяганням, що призведе до зміни об’єму Дотичні ж напруження, як випливає з інших трьох формул системи (3.20), характеризують деформації зсуву. Коефіцієнт l визначає степінь опору середовища зміні об’єму, а m - степінь опору середовища зміні форми.

Поиск по сайту: