Хвильові рівняння

Переміщення пружного тіла 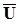можна розкласти на два переміщення і . З першим пов’язана об’ємна деформація q, з другим – оберти v. Доведемо це. Нехай

(4.5)

Вектор обумовлює об’ємну деформацію і не дає обертів. тобто

(4.6)

Вектор дає оберт, але об’ємна деформація відсутня

(4.7)

Перетворимо тепер рівняння (4.4), користуючись відомою формулою з векторної алгебри

, (4.8)

з врахуванням (4.8) рівняння (4.4) приймає вигляд

.(4.9)

Виконаємо операцію дивергенції над рівністю (4.9), беручи до уваги (4.5) та враховуючи, що зовнішні сили дорівнюють нулю. Цей випадок відповідає вільним коливанням пружного середовища, які виникають після припинення дії цих сил.

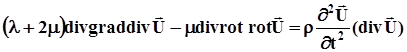
З векторної алгебри відомо, що

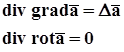
і попереднє рівняння буде

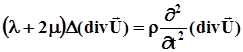
або враховуючи (4.5)

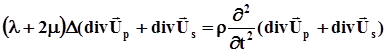
Згідно (4.6) і (4.7)

,

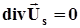
і ми отримаємо рівняння

(4.10)

де

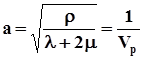
Рівняння (4.10) є хвильовим рівнянням для дилатації q.

Виконаємо тепер операцію ротора над рівністю (4.9)

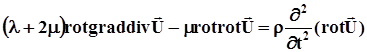
Беручи до уваги, що

,

з попереднього рівняння отримаємо

Але згідно (4.6) і (4.7)

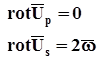
Тепер будемо мати

(4.11)

Перетворимо це рівняння, використовуючи формулу (4.8). Запишемо її у такому вигляді:

(4.12)

Так згідно (4.7)

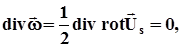
тоді

(4.13)

Таким чином, з врахуванням (4.12) і (4.13) з (4.11) отримаємо

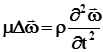
або

(4.14)

де

.

Це хвильове рівняння для обертів .

Поиск по сайту: