Геологічних середовищах

Відомо, що, поширюючись у неідеально пружних середовищах, хвилі диспергують. Причому величина та характер дисперсії фазових швидкостей визначається дисперсійним співвідношенням, однозначно пов’язаним з рівнянням стану середовища. Маючи залежність фазової швидкості від частоти, можна визначити механізм поглинання пружних хвиль і оцінити параметри середовища. Для вирішення цієї задачі необхідні залежності від частоти групової швидкості, яка теж диспергує. У зв'язку з тим, що при наземній сейсморозвідці неможливо отримати залежність групової швидкості від глибини, якщо рахуватися з її дисперсією, нами запропоновано розрахувати параметр дисперсії

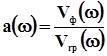(8.1)

де 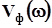- фазова, V_гр - групова швидкості на частоті 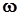. Цей параметр так характеризує середовище: при а< 1 спостерігається аномальна дисперсія швидкості, при а >1 нормальна, при а= 1 дисперсія хвиль відсутня.

Доведено, що для Зовнішньої зони Передкарпатського прогину у продуктивних відкладах Дашавської світи параметр дисперсії а змінюється у межах 0.7 - 1.2. Використання ефективного коефіцієнта затухання пружних хвиль дозволило достатньо чітко прогнозувати продуктивні пласти на Залужанській площі. Це свідчить, що параметр дисперсії а може бути корисним при прогнозуванні геологічного розрізу (ПГР).

У зв'язку з цим, природно ввести миттєвий параметр дисперсії А, який характеризував би дисперсію швидкості пружних хвиль з кроком дискретизації сейсмозапису:

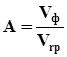, (8.2)

де V_ф - фазова миттєва швидкість, V_гр - миттєва групова швидкість. Оскільки V_ф та V _гр зв'язані з однією миттєвою частотою 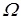, треба відмітити, що параметр А буде так само характеризувати середовище, як і а.

Нагадаємо, що V_ф та V _гр ми визначаємо як

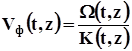
(8.3)

,

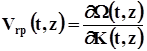де К(t,z) - миттєве або локальне хвильове число. Підставляючи у другий з виразів (8.3) значення миттєвого хвильового числа з першого, для запису з кроком дискретизації Dt, отримаємо:

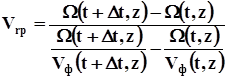(8.4)

Опустимо у формулі (8.4) спільний для всіх членів аргумент z, а за V _гр (t) візьмемо швидкість псевдоакустичного каротажу, яка розраховується за формулою:

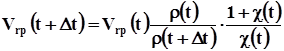, (8.5)

де r(t) - щільність в узгодженому з глибиною масштабі часу, c(t)- залежність коефіцієнту відбиття від часу. Ми не будемо зупинятися тут на методиці визначення r(t) та c(t), яка описана в літературі по псевдоакустичному каротажу (ПАК).

Підставляючи у формулу (8.2) вираз (8.4) з врахуванням, (8.5) отримаємо рекурентне співвідношення:

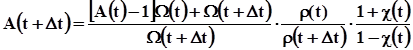
(8.6)

Вираз (8.6) дозволяє послідовно розрахувати трасу параметра дисперсії хвиль, задаючись значенням А(0). Процедура нагадує по технології псевдоакустичний каротаж, у якому задаючись першою акустичною жорсткістю, зверху вниз (від малих часів до великих) розраховують трасу хвильових опорів. Основна складність міститься у виборі А(0). Справа в тому, що з фізичних міркувань дисперсія хвиль тісно пов'язана з поглинанням їх енергії, і у верхній частині розрізу (на малих часах) повинна бути якщо не максимальна, то у всякому випадку значна. При цьому інформації про величину дисперсії у верхній частині розрізу, у нас немає. Разом з тим ми знаємо, що з глибиною значення коефіцієнта поглинання зменшується, а у кристалічних породах фундаменту ними можна знехтувати. Отож і дисперсія з глибиною повинна зменшуватись. Окрім "фізичної" дисперсії хвиль за рахунок непружності середовища, ми повинні рахуватись з дисперсією хвиль, пов'язаною з їх інтерференцією у тонкошаруватому розрізі. Причому остання може значно перевищувати по своїй величині першу. Тому у якості "опорного" необхідно вибирати у розрізі достатньо потужний, однорідний пласт, з низьким коефіцієнтом затухання пружних хвиль. Такий пласт можна вважати абсолютно пружним, а параметр А у ньому рівним 1, оскільки дисперсія хвиль із за непружності або інтерференції у ньому відсутня.

Застосовуючи для розрахунку дисперсії вниз вираз (8.6), а для перерахунку вверх –формулу

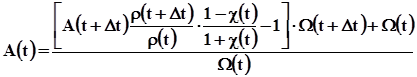
(8.7)

отримаємо трасу параметра дисперсії пружних хвиль. По своєму характеру ця траса миттєвого параметра і вона повинна характеризувати диспергуючі властивості тонкошаруватого середовища.

Формули (8.6), (8.7) не містять похідних по глибині і можуть бути реалізовані для будь-яких модифікацій сейсморозвідки. Оскільки для них, як і для псевдоакустичного каротажу, характерно накопичення помилок, жорсткі вимоги необхідно накласти на ступінь очищення хвильового поля від завад. При цьому необхідно простежити, щоб в граф обробки не включались процедури, які приводять до значних фазових зсувів на всій сейсмотрасі та її окремих ділянках. Ця вимога випливає з того, що параметр дисперсії сильно залежить від миттєвої частоти, яка є похідною по часу миттєвої фази сейсмічного сигналу.

Таким чином., запропонований алгоритм розрахунку миттєвого параметра дисперсії дає можливість вивчення дисперсії пружних хвиль у тонкошаруватих розрізах по даним наземної сейсморозвідки.

Поиск по сайту: