 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Ю.В.Філатов, Ю.Ф.Ткаченко
рівноможливих елементарних подій;
б) відношенню кількості всіх рівноможливих елементарних подій до кількості елементарних подій, що сприяють події;
в) добутку кількості елементарних подій, що сприяють події та кількості всіх рівноможливих елементарних подій;
г) кількості елементарних подій, що сприяють події; д) інша відповідь.
А.
28 Згідно геометричного означення ймовірності, ймовірність події дорівнює:
а) геометричній мірі множини, що задає подію;
б) частці від ділення геометричної міри множини, що задає подію на геометричну міру множини, що задає весь простір елементарних подій;
в) відношенню міри простору елементарних подій до міри події;
г) процентному вмісту події в просторі елементарних подій; д) інша відповідь.
Б.
29 Згідно теореми множення ймовірностей ймовірність добутку двох подій дорівнює:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
В.
30 Ймовірність добутку трьох подій обчислюється за формулою:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Г.
31 Повною групою подій є:
а) набір незалежних рівноймовірних подій;
б) набір несумісних подій, сума яких є достовірною подією;
в) набір незалежних подій, сума яких є достовірною подією;
д) набір подій, сума яких є достовірною подією; д) інша відповідь.
Б.
32 Група подій називається незалежною в сукупності, якщо:
а) кожні дві події з цієї групи незалежні;
б) ймовірність добутку будь-якого скінченого набору подій з групи дорівнює добутку їх ймовірностей;
в) ймовірність добутку всіх подій групи дорівнює добутку їх ймовірностей;
г) ймовірність добутку подій групи дорівнює нулю; д) інша відповідь.
Б.
33 За формулою повної ймовірності ймовірність події  дорівнює (
дорівнює (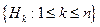 –повна група подій):
–повна група подій):
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
В.
34 Формула Байєса має вигляд ( –повна група подій):
–повна група подій):
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Д.
35 Апостеріорні ймовірності гіпотез можна обчислити за формулою:
а) Байєса; б) Бернуллі; в) Пуассона; г) повної ймовірності; д) інша відповідь.
А.
36 Схемою Бернуллі називається схема проведення експериментів:
а) з підкиданням монети; б) з підкиданням грального кубика;
в) незалежних один від одного; г) однакових і незалежних скінченну кількість раз; д) інша відповідь.
Г.
37 Ймовірність того, що деяка подія в схемі Бернуллі з  випробувань відбудеться
випробувань відбудеться  раз дорівнює (
раз дорівнює ( – ймовірність цієї події в кожному випробуванні):
– ймовірність цієї події в кожному випробуванні):
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
А.
38 Найбільш ймовірною кількістю успіхів в схемі Бернуллі з  випробувань та ймовірністю успіху в кожному з них
випробувань та ймовірністю успіху в кожному з них  є:
є:
а)  ; б)
; б) 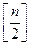 ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Г.
39 При великій кількості випробувань за схемою Бернуллі та малоймовірному успіху в кожному випробуванні ймовірність того, що успіх наступить  раз, може бути наближено обчислена за формулою (
раз, може бути наближено обчислена за формулою ( – кількість випробувань,
– кількість випробувань,  – ймовірність успіху в кожному з них):
– ймовірність успіху в кожному з них):
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
А.
40 Функцією розподілу випадкової величини  є функція:
є функція:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Г.
41 Які з рівностей є правильними ( - функція розподілу випадкової величини
- функція розподілу випадкової величини  )?
)?
1) 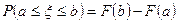 ; 2)
; 2)  ;
;
3)  ;
;
4) 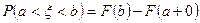 .
.
а) 1 і 3; б) 2 і 4; в) 3 і 4; г) 2 і 3; д) інша відповідь.
Б.
42 Функція розподілу випадкової величини є:
а) неперервною зростаючою функцією; б) неспадною неперервною справа функцією;
в) неспадною неперервною зліва функцією; г) спадною неперервною функцією; д) інша відповідь.
В.
43 Щільність розподілу випадкової величини - це функція  , для якої (
, для якої ( – функція розподілу):
– функція розподілу):
а)  ; б)
; б) 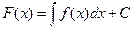 ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Г.
44 Основними властивостями щільності розподілу  є:
є:
а)  ,
,  ; б)
; б)  ,
,  ;
;
в)  ,
, 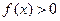 ; г)
; г)  ,
,  ; д) інша відповідь.
; д) інша відповідь.
А.
45 Математичним сподіванням дискретної випадкової величини з розподілом  є:
є:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Б.
46 Які з рівностей для математичного сподівання є неправильними ( - випадкові величини,
- випадкові величини, 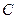 - постійна)?
- постійна)?
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  .
.
а) тільки 5; б) 3 і 4; в) 3 і 5; г) 1, 2 і 4; д) інша відповідь.
В.
47 Чи правильна рівність  ?
?
а) правильна; б) неправильна; в) правильна, якщо  і
і  однаково розподілені.;
однаково розподілені.;
г) правильна, якщо  і
і  незалежні; д) інша відповідь.
незалежні; д) інша відповідь.
Г.
48 Математичне сподівання неперервної випадкової величини з щільністю розподілу  дорівнює:
дорівнює:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
А.
49 Математичне сподівання випадкової величини задає:
а) її найбільш ймовірне значення; б) її середнє значення;
в) її найменш ймовірне значення; г) значення, якого потрібно сподіватись; д) інша відповідь.
Б.
50 Дисперсією випадкової величини  є:
є:
а)  ; б)
; б)  ; в)
; в) 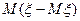 ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Г.
51 Дисперсія випадкової величини характеризує:
а) її відхилення від початку координат; б) її відхилення від середнього значення;
в) квадрат відхилення середнього значення випадкової величини від початку координат;
г) середнє значення різниці випадкової величини та її середнього значення; д) інша відповідь.
Б.
52 Які з рівностей для дисперсії є неправильними ( - випадкові величини,
- випадкові величини, 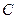 - стала)?
- стала)?
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4) 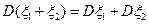 ; 5)
; 5) 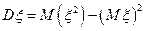 .
.
а) 1, 3 і 4; б) тільки 3; в) 3 і 4; г) 2 і 5; д) інша відповідь.
В.
53 Середньоквадратичне відхилення випадкової величини є:
а) квадратним коренем з дисперсії цієї величини;
б) середнім значенням квадрата цієї величини;
в) відхиленням середнього значення квадрата випадкової величини від її середнього значення;
г) квадратом середнього значення цієї величини; д) інша відповідь.
А.
54 Випадкова величини  має біноміальний розподіл з параметрами
має біноміальний розподіл з параметрами  і
і  . Які із рівностей є абсолютно правильними?
. Які із рівностей є абсолютно правильними?
1) 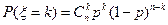 , при
, при  ;
;
2)  ; 3)
; 3) 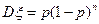 .
.
а) тільки 1; б) тільки 2; в) тільки 3; г) тільки 1 і 2; д) інша відповідь.
Г.
55 Випадкова величини  має розподіл Пуассона з параметром
має розподіл Пуассона з параметром  . Які із рівностей є абсолютно правильними?
. Які із рівностей є абсолютно правильними?
1)  , при
, при  ; 2)
; 2)  ; 3)
; 3)  .
.
а) тільки 1 і 2; б) тільки 1 і 3; в) тільки 2 і 3; г) всі; д) інша відповідь.
А.
56 Випадкова величини  має рівномірний розподіл на відрізку
має рівномірний розподіл на відрізку 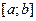 . Які із тверджень є абсолютно правильними?
. Які із тверджень є абсолютно правильними?
1) Її щільність розподілу є кусково сталою; 2) 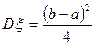 ; 3)
; 3) 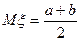 .
.
а) всі; б) тільки 1 і 2; в) тільки 1 і 3; г) тільки 3; д) інша відповідь.
В.
57 Випадкова величини  має нормальний розподіл з параметрами
має нормальний розподіл з параметрами  і
і  . Які із тверджень є абсолютно правильним?
. Які із тверджень є абсолютно правильним?
1)  ,
,  ; 2)
; 2)  ; 3)
; 3) 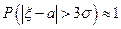 .
.
а) тільки 1 і 2; б) тільки 1 і 3; в) тільки 2 і 3; г) 1, 2 і 3; д) інша відповідь.
А.
58 Випадкова величина  має нормальний розподіл з параметрами
має нормальний розподіл з параметрами  і
і  . Які із тверджень є правильними?
. Які із тверджень є правильними?
1) Щільність розподілу  має вигляд
має вигляд  ;
;
2) щільність розподілу  має вигляд
має вигляд 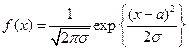 ;
;
3) 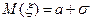 ,
,  ; 4)
; 4)  ,
,  .
.
а) тільки 1; б) тільки 2 і 4; в) тільки 2 і 3; г) тільки 1 і 4; д) інша відповідь.
Г.
59 Які із тверджень правильні для функції Лапласа  ?
?
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4) 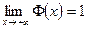 ; 5)
; 5)  .
.
а) 3 і 4; б) 1 і 5; в) 2 і 5; г) 1 і 4; д) інша відповідь.
Б.
60 Функція Лапласа має вид:
а)  ; б)
; б) 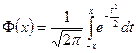 ;
;
в) 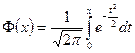 ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
В.
61 Випадкова величина  має показниковий розподіл з параметром
має показниковий розподіл з параметром  . Які із тверджень є правильними?
. Які із тверджень є правильними?
1) Щільність розподілу  має вигляд
має вигляд 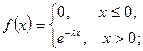
2) щільність розподілу  має вигляд
має вигляд 
3)  ; 4)
; 4)  .
.
а) 2 і 3; б) 1 і 3; в) 2 і 4; г) 1 і 4; д) інша відповідь.
А.
62 Встановити відповідність між щільностями і розподілами.
1)  1) нормальний;
1) нормальний;
2)  2) показниковий;
2) показниковий;
3)  ; 3) рівномірний.
; 3) рівномірний.
а) 1-3, 2-1, 3-2; б) 1-3, 2-2, 3-1; в) 1-1, 2-2, 3-3; г) 1-2, 2-3, 3-1; д) інша відповідь.
Б.
63 Нехай  – коефіцієнт кореляції випадкових величин
– коефіцієнт кореляції випадкових величин  і
і  . Які із тверджень є правильними?
. Які із тверджень є правильними?
1)  , якщо випадкові величини незалежні;
, якщо випадкові величини незалежні;
2) якщо  , то випадкові величини незалежні;
, то випадкові величини незалежні;
3)  тоді і тільки тоді, коли випадкові величини лінійно залежні.
тоді і тільки тоді, коли випадкові величини лінійно залежні.
а) тільки 3; б) тільки 1 і 3; в) тільки 2 і 3; г) тільки 1 і 2; д) інша відповідь.
Б.
64 Коефіцієнтом кореляції двох випадкових величин  і
і  є число рівне:
є число рівне:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Г.
65 Які із наведених значень є параметрами нормального розподілу на площині (двовимірного нормально розподіленого випадкового вектора)?
1) Математичні сподівання кожного з елементів вектора;
2) медіани кожного з елементів вектора;
3) математичне сподівання добутку елементів вектора;
4) коефіцієнт кореляції елементів вектора;
5) коваріація елементів вектора;
6) дисперсії елементів вектора;
7) сума дисперсій елементів вектора.
а) тільки 1, 4 і 7; б) тільки 2, 5 і 4; в) тільки 1, 4 і 6; г) тільки 2, 4 і 6; д) інша відповідь.
В.
66 Згідно із законом великих чисел правильними є такі твердження:
1) Малоймовірно, що середнє арифметичне відхилень випадкових величин від своїх математичних сподівань значно відрізняється від 0, при великій кількості незалежних випадкових величин.
2) Сума великої кількості випадкових величин має приблизно нульове математичне сподівання та одиничну дисперсію.
3) Відносна частота успіху в схемі Бернуллі мало відрізняється від ймовірності успіху в кожному з випробувань, при великій кількості випробувань.
а) тільки 1; б) тільки 2; в) тільки 3; г) тільки 1 і 2; д) інша відповідь.
Д.
67 Нехай  – послідовність незалежних однаково розподілених випадкових величин з математичним сподіванням
– послідовність незалежних однаково розподілених випадкових величин з математичним сподіванням  і дисперсією
і дисперсією  . Які з тверджень є правильними?
. Які з тверджень є правильними?
1)  має стандартний нормальний розподіл;
має стандартний нормальний розподіл;
2)  ;
;
3)  при великих
при великих  має приблизно нормальний розподіл з середнім
має приблизно нормальний розподіл з середнім  і дисперсією
і дисперсією  .
.
4) 
а) тільки 1 і 2; б) тільки 2 і 3; в) тільки 3 і 4; г) тільки 2, 3 і 4; д) інша відповідь.
Б.
68 Нехай  – характеристична функція випадкової величини
– характеристична функція випадкової величини  . В яких із тверджень допущені помилки?
. В яких із тверджень допущені помилки?
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
а) тільки в 1 і 2; б) тільки в 2 і 3; в) тільки в 3 і 4; г) тільки в 1 і 4; д) інша відповідь.
В.
69 Впорядкуйте шкали вимірювань від найпростішої до найбільш багатої.
1) шкала найменувань; 2) шкала порядку; 3) шкала відношень; 4) шкала інтервалів.
а) 1, 2, 3, 4; б) 2, 1, 4, 3; в) 2, 1, 3, 4; г) 1, 2, 4, 3; д) інша відповідь.
Г.
70 Точкова оцінка  параметра
параметра  розподілу генеральної сукупності називається незміщеною конзистентною (слушною) та ефективною, якщо виконуються такі з наведених вимог:
розподілу генеральної сукупності називається незміщеною конзистентною (слушною) та ефективною, якщо виконуються такі з наведених вимог:
1)  ; 2)
; 2)  , при
, при 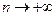 ;
;
3)  , при
, при 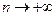 для всіх
для всіх 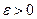 ;
;
4) 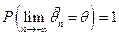 ;
;
5)  є мінімальною серед дисперсій інших оцінок параметра
є мінімальною серед дисперсій інших оцінок параметра  ;
;
6)  є мінімальною серед дисперсій інших незміщених оцінок параметра
є мінімальною серед дисперсій інших незміщених оцінок параметра  .
.
а) 1, 2 і 3 відповідно; б) 1, 3 і 6 відповідно; в) 2, 4 і 6 відповідно; г) 2, 4 і 5 відповідно; д) інша відповідь.
Б.
71 Які з оцінок є оцінками математичного сподівання?
1)  ; 2) медіана; 3)
; 2) медіана; 3)  ; 4) мода.
; 4) мода.
а) тільки 1, 3 і 4; б) тільки 2, 3 і 4; в) тільки 1, 2 і 3; г) тільки 1; д) інша відповідь.
В.
72 Які з оцінок не є оцінками дисперсії генеральної сукупності?
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  .
.
а) тільки 1 і 3; б) тільки 1 і 4; в) тільки 2; г) тільки 4; д) інша відповідь.
Г.
73 Інтервальною оцінкою параметра  розподілу генеральної сукупності з надійністю
розподілу генеральної сукупності з надійністю  є інтервал:
є інтервал:
а)  , для якого
, для якого  ; б)
; б)  , для якого
, для якого  ;
;
в)  , для якого
, для якого  ; г)
; г)  , для якого
, для якого  ; д) інша відповідь.
; д) інша відповідь.
А.
74 Інтервальною оцінкою (надійним інтервалом) для математичного сподівання нормального розподілу з надійністю  є:
є:
а)  , якщо дисперсія
, якщо дисперсія  відома, де
відома, де  – квантиль порядку
– квантиль порядку  розподілу Стьюдента з
розподілу Стьюдента з  ступенем вільності (свободи);
ступенем вільності (свободи);
б)  , якщо дисперсія
, якщо дисперсія  невідома, де
невідома, де  – квантиль порядку
– квантиль порядку  стандартного нормального розподілу; в)
стандартного нормального розподілу; в)  , якщо дисперсія
, якщо дисперсія  відома, де
відома, де  – квантиль порядку
– квантиль порядку  стандартного нормального розподілу;
стандартного нормального розподілу;
г) 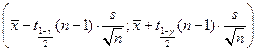 , якщо дисперсія
, якщо дисперсія  невідома, де
невідома, де  – квантиль порядку
– квантиль порядку  розподілу Стьюдента з
розподілу Стьюдента з  ступенем вільності (свободи);
ступенем вільності (свободи);
д) інша відповідь.
В.
75 Інтервальною оцінкою (надійним інтервалом) з надійністю  для дисперсії нормального розподілу є (
для дисперсії нормального розподілу є ( – квантиль порядку
– квантиль порядку  розподілу Пірсона (
розподілу Пірсона (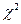 ) з
) з  ступенями вільності (свободи)):
ступенями вільності (свободи)):
а)  ; б)
; б) 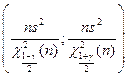 ; в)
; в) 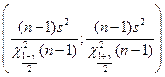 ;
;
г) 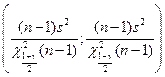 ; д) інша відповідь.
; д) інша відповідь.
Г.
76 Яке з тверджень щодо перевірки статистичних гіпотез є помилковим?
1) Помилкою першого типу є відхилення правильної гіпотези;
2) помилкою другого типу є підтвердження неправильної гіпотези;
3) перевірка статистичної гіпотези є логічним доведенням її правильності чи хибності;
4) для кожної статистичної гіпотези існує альтернативна гіпотеза.
а) тільки 1; б) тільки 2; в) тільки 3; г) тільки 4; д) інша відповідь.
В.
77 Основна гіпотеза підтверджується, якщо вибіркове значення статистики критерію:
а) менше критичного значення; б) більше критичного значення;
в) попадає в критичну область; г) не попадає в критичну область; д) інша відповідь.
Г.
78 Рівнем значущості критерію перевірки статистичної гіпотези є:
а) ймовірність того, що результат перевірки буде правильним;
б) ймовірність помилки першого роду; в) ймовірність помилки другого роду;
г) максимальне відхилення вибіркового значення статистики критерію від критичного; д) інша відповідь.
Б.
79 Критичним значенням критерію Пірсона перевірки гіпотези про розподіл генеральної сукупності при рівні значущості  є (
є ( – кількість інтервалів,
– кількість інтервалів,  – кількість параметрів розподілу оцінених за вибіркою):
– кількість параметрів розподілу оцінених за вибіркою):
а) квантиль порядку 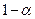 розподілу Пірсона (
розподілу Пірсона (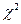 ) з
) з  ступенем вільності (свободи);
ступенем вільності (свободи);
б) квантиль порядку  розподілу Пірсона (
розподілу Пірсона (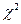 ) з
) з  ступенем вільності (свободи);
ступенем вільності (свободи);
в) квантиль порядку 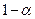 розподілу Пірсона (
розподілу Пірсона (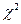 ) з
) з  ступенем вільності (свободи);
ступенем вільності (свободи);
г) квантиль порядку  розподілу Пірсона (
розподілу Пірсона (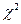 ) з
) з  ступенем вільності (свободи); д) інша відповідь.
ступенем вільності (свободи); д) інша відповідь.
А.
80 Які із тверджень правильні?
1) Точковою оцінкою коефіцієнта кореляції випадкових величин  і
і  є
є  , де
, де  – вибіркове середнє значень величини
– вибіркове середнє значень величини  ,
,  – вибіркове середнє значень величини
– вибіркове середнє значень величини  ,
,  – вибіркове середнє значень величини
– вибіркове середнє значень величини  ,
, 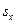 та
та  – вибіркові середньоквадратичні відхилення випадкових величин
– вибіркові середньоквадратичні відхилення випадкових величин  і
і  відповідно;
відповідно;
2) рівність нулю точкової оцінки коефіцієнта кореляції двох випадкових величин свідчить про їх некорельованість;
3) відмінність від нуля точкової оцінки коефіцієнта кореляції двох випадкових величин свідчить про їх залежність;
4) вибірковий коефіцієнт кореляції лежить в межах від  до
до  .
.
а) тільки 2 і 3; б)тільки 3 і 4; в) тільки 1, 3 і 4; г) тільки 1 і 4; д) інша відповідь.
Г.
81. Залежність випадкової величини  від значень невипадкової величини
від значень невипадкової величини  називається лінійною регресією
називається лінійною регресією  на
на  , якщо:
, якщо:
а)  ; б) відхилення величини
; б) відхилення величини  від
від  є мінімальними;
є мінімальними;
в) середнє значення величини  при кожному значенні
при кожному значенні  дорівнює
дорівнює  ;
;
г) середнє значення величини  дорівнює
дорівнює  ; д) інша відповідь.
; д) інша відповідь.
В.
82 Дисперсійний аналіз є методом перевірки гіпотези про:
а) рівність дисперсії генеральної сукупності даному числу;
б) рівність дисперсій кількох генеральних сукупностей;
в) рівність математичних сподівань кількох генеральних сукупностей;
г) задані значення математичних сподівань кількох генеральних сукупностей;
д) інша відповідь.
В.
83 Нехай  – результати спостережень за значеннями випадкової величини
– результати спостережень за значеннями випадкової величини  при значеннях
при значеннях  незалежної змінної
незалежної змінної  . Точкові оцінки параметрів лінійної регресії
. Точкові оцінки параметрів лінійної регресії  на
на  знаходимо із системи рівнянь:
знаходимо із системи рівнянь:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Б.
84 Нехай  надійний інтервал з надійністю
надійний інтервал з надійністю  для параметра
для параметра  розподілу генеральної сукупності, причому
розподілу генеральної сукупності, причому  . Основна гіпотеза
. Основна гіпотеза  , альтернативна гіпотеза
, альтернативна гіпотеза  . В якому випадку основа гіпотеза узгоджується із вибірковими даними і який рівень значущості
. В якому випадку основа гіпотеза узгоджується із вибірковими даними і який рівень значущості  критерію?
критерію?
а)  ,
, 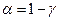 ; б)
; б)  ,
,  ;
;
в)  ,
, 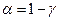 ; г)
; г)  ,
,  ; д) інша відповідь.
; д) інша відповідь.
А.
85 Нехай  надійний інтервал з надійністю
надійний інтервал з надійністю  для параметра
для параметра  розподілу генеральної сукупності, причому
розподілу генеральної сукупності, причому  . Основна гіпотеза
. Основна гіпотеза  , альтернативна гіпотеза
, альтернативна гіпотеза  . В якому випадку основа гіпотеза узгоджується із вибірковими даними і який рівень значущості
. В якому випадку основа гіпотеза узгоджується із вибірковими даними і який рівень значущості  критерію?
критерію?
а)  ,
,  ; б)
; б)  ,
,  ; в)
; в)  ,
, 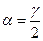 ; г)
; г)  ,
,  ; д) інша відповідь.
; д) інша відповідь.
Г.
рівень C
1 Задано множину чисел {1,2,3,4,5}. Числа навмання розміщують в рядок. Яка ймовірність того, що при цьому утвориться парне п'ятицифрове число?
а)  ; б)
; б) 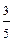 ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
А.
2 У групі 15 студентів, серед яких 8 відмінників. Навмання вибрано 9 студентів. Знайти ймовірність того, що серед вибраних студентів буде 6 відмінників.
а) 0,191; б) 0,196; в) 0,201; г) 0,206; д) інша відповідь.
Б.
3 Переможцями конкурсу стали 3 жінок та 4 чоловіків. Організатори випадковим чином обрали 4 особи для вручення суперпризів. Яка ймовірність того, що серед них буде дві жінки і два чоловіка?
а)  ; б)
; б) 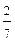 ; в)
; в) 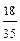 ; г)
; г) 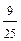 ; д) інша відповідь.
; д) інша відповідь.
В.
4 В аудиторії серед 15 комп'ютерів 12 справних. Знайти ймовірність того, що з двох вибраних комп'ютерів хоча б один виявиться несправним.
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Г.
5 Один раз підкидають три гральних кубики. Яка ймовірність того, що на різних кубиках випаде різна кількість очок?
а) 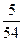 ; б)
; б)  ; в)
; в)  ; г)
; г) 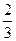 ; д) інша відповідь.
; д) інша відповідь.
Б.
6 Один раз підкидають три гральних кубики. Яка ймовірність того, що на всіх кубиках випаде однакова кількість очок?
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Г.
7 Один раз підкидають три гральних кубики. Яка ймовірність того, що хоча б на двох кубиках випаде однакова кількість очок?
а)  ; б)
; б) 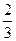 ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
В.
8 Серед 20 ламп 5 бракованих. Знайти ймовірність того, що із чотирьох взятих навмання ламп всі будуть доброякісні.
а) 0,306; б) 0,282; в) 0,243; г) 0,328; д) інша відповідь.
Б.
9 Серед 20 ламп 5 бракованих. Навмання взято 4 лампи. Яка ймовірність того, що серед взятих буде хоча б одна бракована?
а) 0,682; б) 0,754; в) 0,818; г) 0,746; д) інша відповідь.
Д.
10 12 осіб шикуються в шеренгу довільним чином. Знайти ймовірність того, що дві певні особи будуть стояти поруч.
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
А.
11 Номер випадково взятого автомобіля чотирицифровий. Знайти ймовірність того, що номер не містить однакових цифр.
а) 0,021; б) 0,185; в) 0,504; г) 0,625; д) інша відповідь.
В.
12 Номер випадково взятого автомобіля чотирицифровий. Знайти ймовірність того, що номер містить дві однакові цифри.
а) 0,216; б) 0,432; в) 0,648; г) 0,504; д) інша відповідь.
Б.
13 В урні є 12 кульок, з них 8 червоних і 4 чорних. Навмання вибирають 6 кульок. Яка ймовірність того, що вибрано дві чорних кульки?
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Г.
14 В урні є 12 кульок, з них 8 червоних і 4 чорних. Навмання вибирають 6 кульок. Яка ймовірність того, що вибрано хоча б одну чорну кульку?
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Г.
15 В урні є 15 червоних, 9 синіх та 6 зелених кульок. Навмання вибирають 6 кульок. Знайти ймовірність того, що буде вийнято 1 зелену, 2 синіх і 3 червоних кульки?
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 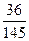 ; д) інша відповідь.
; д) інша відповідь.
В.
16 Числа 1,2,3,…,9 записуються в ряд у випадковому порядку. Знайти ймовірність того, що числа 1 і 2 стоять поруч і в порядку зростання.
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Б.
17 Числа 1,2,3,…,9 записуються в ряд у випадковому порядку. Знайти ймовірність того, що числа 3, 6 і 9 будуть стояти поруч в довільному порядку.
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
А.
18 Із урни, в якій є 2 білі, 3 чорні і 5 червоних кульок, навмання взято три кульки. Знайти ймовірність того, що серед взятих кульок хоча б дві будуть одного кольору.
а) 0,5; б) 0,25; в) 0,8; г) 0,75; д) інша відповідь.
Г.
19 Числа 1,2,3,…,9 записуються в ряд у випадковому порядку. Знайти ймовірність того, що на місцях з парними номерами стоятимуть парні числа.
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 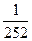 ; д) інша відповідь.
; д) інша відповідь.
В.
20 У шафі стоять 5 пар різних розмірів. З них навмання вибирають 4 чоботи. Знайти ймовірність того, що серед вибраних чобіт жоден не має пари.
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Б.
21 У колі радіусом 5 см розташовано прямокутник зі сторонами 4 см і 6 см. Яка ймовірність того, що навмання вибрана всередині кола точка лежатиме і всередині прямокутника?
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Д.
22 Навмання обрано два додатних числа x та y, кожне з яких не перевищує 7. Знайти ймовірність того, що сума їх буде не більша 5.
а) 0,255; б) 0,260; в) 0,265; г) 0,270; д) інша відповідь.
А.
23 У квадрат з вершинами А(0;0), В(1;0), С(1;1), Д(0;1) навмання кинуто точку М(p;q). Знайти ймовірність того, що корені рівняння  будуть дійсними.
будуть дійсними.
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
В.
24 На відрізку [-1;2] навмання взято два числа. Яка ймовірність того, що їх сума більша за 1, а добуток менший за 1?
а) 0,384; б) 0,321; в) 0,285; г) 0,416; д) інша відповідь.
Б.
25 Всередину круга кинуто точку. Знайти ймовірність того, що вона потрапить у вписаний в цей круг квадрат.
а) 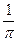 ; б)
; б) 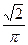 ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
В.
26 Навмання вибирається число, яке міститься між нулем і одиницею. Знайти ймовірність того, що це число буде не менше від 0,25 і не більше від 0,75.
а) 0,75; б) 0,4; в) 0,5; г) 0,25; д) інша відповідь.
В.
27 На відрізку [-1;1] навмання беруть два числа. Знайти ймовірність того, що сума квадратів цих чисел буде не більша за 1.
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
А.
28 Між нулем і одиницею навмання вибирають два числа. Знайти ймовірність того, що сума цих чисел буде не більша за 1, а модуль їх різниці не менший від ½.
а)  ; б)
; б)  ; в)
; в) 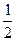 ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Б.
29 На відрізок довжиною  навмання кинуто дві точки. Знайти ймовірність того, що віддаль між цими точками буде не менша від
навмання кинуто дві точки. Знайти ймовірність того, що віддаль між цими точками буде не менша від  .
.
а) 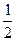 ; б)
; б)  ; в)
; в)  ; г)
; г) 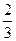 ; д) інша відповідь.
; д) інша відповідь.
Д.
30 На відрізок довжиною  навмання вибирають дві точки. Знайти ймовірність того, що віддаль між цими точками буде не більша від
навмання вибирають дві точки. Знайти ймовірність того, що віддаль між цими точками буде не більша від  .
.
а) 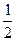 ; б)
; б)  ; в)
; в)  ; г)
; г) 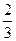 ; д) інша відповідь.
; д) інша відповідь.
В.
31 Диспетчер обслуговує три лінії. Ймовірність того, що протягом години звернуться по першій лінії, становить 0,3, по другій – 0,4, по третій – 0,6. Яка ймовірність того, що протягом години диспетчер отримає виклики з двох ліній?
а) 0,314; б) 0,324; в) 0,334; г) 0,344; д) інша відповідь.
Б.
32 Ймовірність вчасного повернення кредиту для першої фірми складає 0,9 другої – 0,88. Яка ймовірність, що вчасно поверне кредит тільки одна фірма?
а) 0,900; б) 0,088; в) 0,196; г) 0,108; д) інша відповідь.
В.
33 Кондуктор автобуса зберігає купюри різної вартості у двох кишенях: в одній 7 купюр по 2 грн. та 3 купюри по 5 грн., в іншій – відповідно 12 та 8 купюр. З кожної кишені кондуктор навмання дістає одну купюру. Яка ймовірність того, що обидві купюри однієї вартості?
а) 0,42; б) 0,18; в) 0,12; г) 0,54; д) інша відповідь.
Г.
34 Три аварійні пристрої працюють незалежно і сповіщають про аварію з ймовірностями 0,8; 0,9; 0,75. Яка ймовірність того, що при аварії спрацює хоча б один пристрій?
а) 0,975; б) 0,980; в) 0,985; г) 0,990; д) інша відповідь.
Д.
35 Ймовірність одержання студентом оцінки “відмінно” на іспиті дорівнює 0,2. яка ймовірність того, що оцінку “відмінно” одержить не більше як один студент із трьох?
а) 0,896; б) 0,64; в) 0,384; г) 0,512; д) інша відповідь.
А.
36 В ящику 10 білих та 5 чорних куль. Навмання виймають дві кулі. Яка ймовірність того, що чорних куль буде не більше одної?
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Г.
37 Студент вивчив 20 із 25 питань програми. Яка ймовірність того, що він складе екзамен, якщо для цього потрібно відповісти не менше ніж на два із трьох заданих екзаменатором запитань?
а) 0,413; б) 0,909; в) 0,496; г) 0,755; д) інша відповідь.
Б.
38 В електричному колі послідовно з’єднані чотири елементи. Ймовірність виходу з ладу кожного з цих елементів однакова і дорівнює 0,2. Знайти ймовірність того, що струму в колі не буде, тобто вийде з ладу хоча б один елемент.
а) 0,4096; б) 0,9984; в) 0,5904; г) 0,7836; д) інша відповідь.
В.
39 Ймовірність невлучання у мішень першого стрільця дорівнює 0,2, другого – 0,1 і третього – 0,3. Знайти ймовірність влучення в мішень хоча б одним стрільцем.
а) 0,994; б) 0,504; в) 0,092; г) 0,728; д) інша відповідь.
А.
40 Ймовірність того, що під час трьох незалежних випробувань деяка подія настане принаймні один раз, дорівнює 0,875. Знайти ймовірність настання цієї події під час одного випробування, якщо вона під час усіх випробувань однакова.
а) 0,25; б) 0,125; в) 0,6; г) 0,5; д) інша відповідь.
Г.
41 Тираж популярної газети друкується в двох типографіях. Потужності цих типографій відносяться як 3:4, причому перша дає 3,5% браку, друга – 2,5%. Яка ймовірність того, що навмання обраний примірник газети буде бракованим?
а) 0,0293; б) 0,0298; в) 0,0303; г) 0,0308; д) інша відповідь.
А.
42 Виробництво певної продукції може проводитись в двох температурних режимах з ймовірностями 0,45 і 0,55 відповідно. Залежно від температурного режиму ймовірність отримання продукції вищої якості становить 0,8 і 0,9. Яка ймовірність того, що навмання вибрана продукція вищої якості?
а) 0,850; б) 0,855; в) 0,860; г) 0,865; д) інша відповідь.
Б.
43 В групі спортсменів 20 лижників і 4 легкоатлети. Ймовірність виконати норму майстра спорту для кожної групи спортсменів дорівнює відповідно 0,9; 0,75. Яка ймовірність того, що навмання вибраний спортсмен виконає норму майстра спорту?
а) 0,865; б) 0,870; в) 0,875; г) 0,880; д) 0,885.
В.
44 Продуктивність першого автомата вдвічі перевищує продуктивність другого. Перший автомат в середньому дає 60% деталей відмінної якості; другий – 84%. Яка ймовірність того, що навмання вибрана деталь буде з браком?
а) 0,65; б) 0,28; в) 0,4; г) 0,32; д) інша відповідь.
Г.
45 Податкові інспектори роблять перевірку діяльності підприємств: перший обслуговує 40 підприємств, серед яких 25% не мають заборгованостей, другий – 60 підприємств, із них 40% – без заборгованостей, Яка ймовірність того, що навмання обране підприємство не має заборгованості?
а) 0,24; б) 0,29; в) 0,44; г) 0,39; д) інша відповідь.
Д.
46 Завод випускає кухонні набори білого і синього кольорів, що виготовляються двома цехами. Перший цех виробляє 35% продукції, серед яких 40% наборів синього кольору. У продукції другого цеху 55% синіх наборів. Яка ймовірність того, що навмання вибраний набір синього кольору?
а) 0,4975; б) 0,4980; в) 0,4985; г) 0,4990; д) інша відповідь.
А.
47 До каси підприємства надійшли банкноти у пачках від двох банків: 50 пачок від першого і 70 – від другого. Ймовірність помилки касирів першого банку становить 0,0015, другого – 0,002. Яка ймовірність того що навмання вибрану пачку сформовано без помилок?
а) 0,9987; б) 0,9982; в) 0,9977; г) 0,9972; д) інша відповідь.
Б.
48 Два верстати виготовляють деталі, які поступають на конвеєр. З першого верстата надійшло 400 деталей, а з другого на 50% більше. Перший верстат дає 2% браку, другий – 3%. Знайти ймовірність того, що навмання взята деталь з конвеєра є бракованою.
а) 0,016; б) 0,021; в) 0,026; г) 0,031; д) інша відповідь.
В.
49 В першому ящику 5 білих і 10 чорних кульок, в другому – 3 білих і 7 чорних кульок. З другого ящика в перший переклали кульку, а потім з першого ящика витягли навмання одну кульку. Визначити ймовірність того, що витягнута кулька – біла.
Поиск по сайту: