Головні вісі деформації

Доведемо, що в пружному тілі в кожній точці можна виділити три взаємо перпендикулярні прямі, яким властиво наступне. Частинки пружного тіла, які знаходяться до деформації на цих прямих, залишаються на них і після деформації, тобто переміщуються виключно вздовж цих прямих. Ці прямі називаються головними вісями деформації.

Припустимо, що точка А, яка визначається до деформації вектором з складовими x, y, z, знаходиться на одній з головних вісей деформації та її переміщення співпадає з направленням вектора . Цю умову можна записати таким чином:

,

або в координатній формі

, (1.13)

де l -неозначений множник.

Складові вектора визначаються системою (1.9). З врахуванням (1.13) ця система набуде вигляду:

(1.14)

Система (1.14) являє собою систему однорідних лінійних рівнянь відносно невідомих x, y, z. Останні є складовими вектора , в напрямку якого відбувається переміщення . Таким чином, визначення напрямку однієї з головних вісей деформації зводиться до рішення системи (1.14) відносно x, y, z.

Система (1.14) має ненульові рішення при умові

Ця умова приводить до рівняння третьої ступені відносно l. Корені цього рівняння дійсні, позначимо їх через Послідовна підстановка значень в (1.14) дає складові x₁, y₁, z₁, x₂, y₂, z₂ i x₃, y₃, z₃ трьох векторів, i 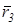які визначають напрямки головних вісей деформації в даній точці.

Покажемо, що головні вісі деформації взаємно перпендикулярні.

Підставимо в (1.14)

, (1.15)

де x₁, y₁, z₁ - рішення системи (1.14) при . Так само можна записати

(1.16)

Помножимо перше з рівнянь (1.15) на x _2, друге на y ₂, третє на z ₂ та просумуємо їх

(1.17)

Помножимо перше з рівнянь (1.16) на x _1, друге на y ₁, третє на z ₁ та знайдемо їх суму

(1.18)

Праві частини рівнянь (1.17) та (1.18) рівні, тому, віднімаючи з першого друге, отримаємо

(1.19)

Оскільки , то з (1.19) виплаває

,

або в векторній формі

.

Рівність нулю скалярного добутку векторів 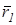та свідчитьть про те, що ці вектори взаємно перпендикулярні. Таким чином, головні вісі деформації, напрямок яких визначаються векторами ₁ та ₂, взаємно перпендикулярні.

Аналогічно можна довести перпендикулярність решти головних вісей деформації.

Позначимо знайдені напрямки трьох взаємно перпендикулярних вісей деформації через 1, 2, 3 та приймемо вісі деформації за вісі координат. У системі координат 1, 2, 3 вираз (1.9) набуває вигляду:

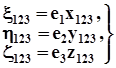(1.20)

де

Індекси 1, 2, 3 означають, що складові вектора 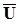взяті відносно вісей 1, 2, 3 та продиференційовані по тих же вісях. Індекс ₁₂₃ означає, що складові векторів та також взяті відносно вісей 1, 2, 3. Формули (1.20) показують, що вісі 1, 2, 3 - головні вісі деформації. Дійсно, з (1.20) слідує, що точка, яка знаходилась до деформації на одній з цих вісей, наприклад, 1, тобто мала координати x ₁₂₃, y ₁₂₃= z ₁₂₃= 0, і після деформації лишається на тій же вісі, оскільки згідно (1.20)

Таким чином, при переході до головних вісей координат 1, 2, 3 компоненти перетворюються в нулі, а компоненти отримують деякі нові значення . Величини називаються головними коефіцієнтами деформації.