Внутрішні напруження

Пружне середовище під дією прикладених до неї зовнішніх сил набуває деформації. При цьому всередині середовища в результаті взаємодії її частин розвиваються внутрішні сили. Вони протидіють зовнішнім силам і намагаються врівноважити їх. Ці внутрішні сили називають пружними напруженнями.

Візьмемо площадку , що містить точку М, у вигляді трикутника і з допомогою трьох взаємоперпендикулярних площин утворимо малий тетраедр об’єму . Осі координат направимо по ребрах тетраедра (рисунок 2.2).

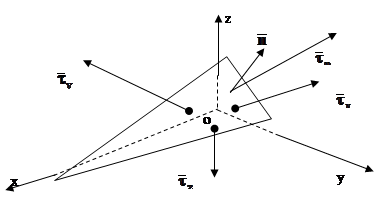Рисунок 2.2 – До умови рівноваги напружень

Позначимо через , , вектори напружень на гранях, перпендикулярних до осей 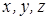. Для рівноваги виділеного з пружного середовища безмежно малого елемента необхідно, щоб сила, прикладена до площадки , дорівнювала геометричні сумі сил, діючих на інші грані. Враховуючи, що сили, прикладені до кожної грані, дорівнюють добутку її площі на напруження, умова рівноваги приймає вигляд:

(2.1)

Векторне рівняння (2.1) можна замінити трьома скалярними:

(2.2)

де , (2.3)

- проекції векторів напружень на осі координат. Перший індекс в (2.3) вказує орієнтацію граней, другий – напрямок компоненти вектора напружень. Величини називаються нормальними компонентами напружень, а 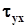, , 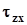, , 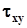, 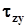- дотичними (тангенціальними) компонентами напружень на площадки, перпендикулярні до осей. Нижче буде доведено, що , , .

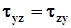Отже, дев’ять компонент напружень (2.3), які визначають напружений стан в точці та її малому околі, залежать від напрямку нормалі в цій точці.

Поиск по сайту: