Головними коефіцієнтами

Встановимо взаємозв’язок між компонентами малої деформації при переході від системи координат x, y, z до системи 1, 2, 3, вісі якої суміщені з головними вісями деформації.

Позначимо косинуси кутів між віссю 1 та вісями x, y, z через 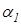, , , віссю 2 з тими же вісями , , , 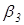віссю 3 також з вісями x, y, z через , , . Ці позначення зведемо в таблицю.

Таблиця 1.1 - Спрямовуючі косинуси координатних

вісей

Вісі	x	y	z
				’
				’
				’
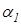
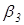
				Орти

Позначимо напрямки вісей x, y, z одиничними векторами 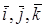, а вісей 1, 2, 3 - векторами . Зрозуміло, що таблиця косинусів в той же час є таблицею складових векторів 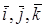по осях 1, 2, 3 та векторів по вісях x, y, z.

У системі координат x, y, z складові вектора визначаються виразом (1.9):

У системі координат 1, 2, 3 складові вектора можна записати у відповідності до (1.20):

Представимо складові вектора по вісях x, y, z як скалярні добутки вектора на вектора , які потім розгорнемо по складовим векторів на вісі 1, 2, 3. В результаті отримаємо:

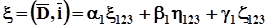(1.21)

(1.22)

(1.23)

Таким самим чином можна представити складові вектора по вісях x, y, z. Розгорнувши скалярні добутки вектора на вектори по складовим цих векторів на вісі 1, 2, 3, отримаємо:

(1.24)

На підставі (1.21), (1.24), та (1.20) перше рівняння системи (1.9) можна представити у вигляді:

або

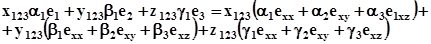
Останній вираз мусить задовольнятись при довільних значеннях x ₁₂₃, y ₁₂₃, z _123. Це означає, що коефіцієнти при x₁₂₃, y₁₂₃, z ₁₂₃ в правій та лівій частинах рівні між собою, тобто

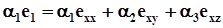(1.25)

(1.26)

(1.27)

З рівнянь (1.25) - (1.27) можна отримати, використовуючи добутки спрямовуючих косинусів з таблиці 1.1,

(1.28)

(1.29)

. (1.30)

Так само можна встановити зв’язок між компонентами деформації та головними коефіцієнтами . Для цього необхідно підставити в друге та третє рівняння системи (1.9) значення та з (1.22) та ( 1.23), x, y, z з (1.24) та з (1.20). В результаті отримаємо

(1.31)

(1.32)

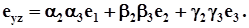(1.33)

Формули (1.28) - (1.33) пов’язують компоненти малої деформації відносно довільних вісей x, y, z через головні коефіцієнти деформації та косинуси кутів між цими вісями та головними вісями деформації.

Поиск по сайту: