Пружні потенціали

Введемо тепер у розгляд допоміжні функції – потенціали.

Вектор зв’я заний умовою

Цій умові можна задовольнити, прийнявши

, (4.15)

де - скалярна функція.

З векторної алгебри відомо, що для скалярної функції

Функція , яка задовольняє рівнянню (4.15), називається потенціальною, а j – скалярним потенціалом силового поля. В задачах теорії пружності j називають також поздовжнім потенціалом або потенціалом поздовжньої хвилі.

Покажемо, що скалярний потенціал задовольняє хвильовому рівнянню (4.10):

Оскільки

то рівняння (4.10) прийме вигляд

або

,

або змінивши порядок диференціювання

Для виразу у круглих дужках можна прийняти

(4.16)

Отримане рівняння для скалярного потенціалу j є рівняння хвильового типу.

Розглянемо переміщення в пружньому тілі, які не супроводжуються обертами. В цьому випадку та і векторне рівняння руху (4.9) прийме вигляд

.

Оскільки згідно (4.8)

,

то зміщення задовольняють хвильовому рівнянню

(4.17)

Всі три рівняння: для дилатації (4.10), для скалярного потенціалу (4.16) і для пружних зміщень (4.17) описують процес розповсюдження поздовжньої хвилі.

З іншого боку, розглянемо вектор з обмеженням , що означає відсутність при деформаціях зміни елементарних об’ємів тіла. Вектор такого поля переміщень можна визначити через ротор векторної функції :

(4.18)

для якої

Вектор називають векторним потенціалом або потенціалом поперечної хвилі. Поле такого вектора називається вихровим.

Підставляючи (4.18) в рівняння руху (4.9)

і враховуючи, що та згідно (4.8)

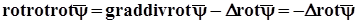
отримаємо

(4.19)

Виконаємо над (4.19) операцію rot і, змінивши порядок диференційних операцій, отримаємо

(4.20)

Згідно (4.8) і рівняння (4.20) прийме вигляд

звідки

.

Ми задовольнимо цьому рівнянню, якщо покладемо

(4.21)

Повертаючи (4.14), (4.21) і (4.22), робимо висновок, що всі три рівняння однотипні і описують процес розповсюдження поперечної хвилі.

Отже, представляючи векторну функцію й у вигляді суми

, (4.23)

де і - скалярний та векторний потенціали, рівняння руху ізотропного однорідного пружного середовища (4.4) розкладається на два незалежних руху. Перший з них пов’язаний із зміною елементарних об’ємів речовини – стисненням або розтягом – і відповідає поздовжній хвилі. Для другого характерні оберти елементарних об’ємів, а розповсюдження цього виду деформації відповідає поперечній хвилі. Таким чином, з кожним типом хвиль пов’язаний певний вид пружної деформації. Швидкість розповсюдження окремого типу деформації залежить від коефіцієнтів а і b, хвильових рівнянь:

;

.

Відношення

(4.24)

і залежить від коефіцієнта Пуассона . Це означає, що поздовжня хвиля розповсюджується з більшою швидкістю ніж поперечна.

Для більшості гірських порід коефіцієнт Пуассона змінюється в границях 0,15< <0,5.

Наприклад, для =0,25 (гіпотеза Пуассона) , що відповідає міцним матеріалам (сталь, скло) і породам на значній глибині.

Поиск по сайту: