Границі двох середовищ

Встановимо залежність між амплітудами відбитої, заломленої і падаючої хвиль поблизу границь двох пружних середовищ. Співвідношення, що визначають амплітуди відбитих хвиль порівняно з амплітудою падаючої хвилі, називаються коефіцієнтами відбиття, а співвідношення, які визначають амплітуди проходячих хвиль порівняно з амплітудою падаючої хвилі – коефіцієнтами проходження (або заломлення).

Рішення задачі обмежимо випадком нормального падіння плоскої хвилі на плоску границю двох пружних середовищ.

У випадку нормального падіння фазові поверхні плоскої хвилі паралельні плоскій границі розділу (рисунок 5.1). Розмістимо прямокутну систему координат x, y, z так, щоб площина XOY співпадала з границею розділу . Вісь z спрямуємо вертикально вниз. Тоді, очевидно, достатньо розглянути хвильову картину в напрямку вісі z, так як в площині XOY і у всіх паралельних її площин зміщення знаходиться в однакових фазах і мають постійну величину. Таким чином у випадку нормального падіння хвильове поле залежить тільки від однієї просторової координати z.

М

Рисунок 5.1 – Плоска хвиля на границі двох середовищ

1. Граничні умови та основні рівняння. Коливання середовищ, що мають граничні поверхні , залежать від режиму, який виконується на цих поверхнях. Умови на границях реальних геологічних середовищ рахуються такими, що при переході через них залишаються неперервними значення векторів зміщення і напруження. Такі контакти середовищ називаються жорсткими.

Побудуємо в кожній точці М поверхні одиничну нормаль та будемо розрізняти додатну (+) та від’ємну (-) сторони цієї поверхні. По різні боки від границі виберемо точки М ⁺ і М ^-, нескінченно близькі до точки М. Тоді умови жорсткості контакту математично можна записати у вигляді

(5.1)

(5.2)

Знайдемо складові векторів зміщення і напруження для випадку, коли поле зміщення залежить від однієї просторової координати z.

Поле зміщення виражається через потенціали і по загальній формулі

в якій підпорядкований додатковій умові .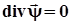

Для вектору зміщення поздовжньої хвилі отримуємо

(5.3)

Поле зміщення поперечної хвилі доцільно розглядати як накладання хвиль SV i SH, тобто

.

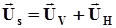Поперечна хвиля SV характеризується тим, що вона поляризована на площині променів. Якщо площиною променів є площина XOZ, то векторний потенціал хвилі SV має вигляд

тобто перпендикулярний площині променів.

Складова зміщення хвилі SV визначається на підставі формули

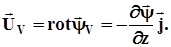(5.4)

Поперечна хвиля SV поляризована в площині, яка перпендикулярна площині падіння. ЇЇ векторний потенціал лежить в площині падіння і представляється формулою

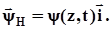
Складова зміщень хвилі SН визначається на підставі формули

(5.5)

Для визначення складових вектора напруження

на площинах z=const необхідно скористатися формулами

(5.6)

Відбиття – заломлення хвиль на границі розділу можна розкласти на два незалежних процеси: на відбиття – заломлення повздовжньої або поперечної SV хвиль, в результаті якого утворюються тільки повздовжні або поперечні SV хвилі, і на відбиття – заломлення поперечної SН хвилі, в результаті якого утворюються хвилі тільки типу SН.

Якщо поле зміщень визначається поздовжніми 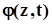і поперечними потенціалами, то, враховуючи формули (5.3) і (5.4), маємо для складових вектора зміщення

наступні формули

(5.7)

Підставляємо (5.7) в (5.6), отримаємо такі ж формули для складових вектора напруження

(5.8)

У випадку поля поперечної SН хвилі, що характеризується вектором зміщення (5.5), маємо

(5.9)

Підставляючи (5.9) в (5.6), отримаємо також формули для складових вектора напруження :

(5.10)

Поиск по сайту: