Плоских хвиль

Нехай два пружних півпростори (1 і 2) знаходяться у жорсткому контакті один з одним. Властивості півпросторів будемо характеризувати сталими V_p1, V_s1, r₁ і V_p2, V_s2, r₂, причому .

Площина Z=0 співпадає з границею розділу півпросторів 1 і 2, а вісь Z спрямуємо з середовища 1 в середовище 2.

У випадку нормального падіння плоскої поздовжньої хвилі виникають тільки поздовжні вторинні хвилі, а у випадку нормального падіння поперечної хвилі виникають тільки поперечні вторинні хвилі.

Нехай з середовища 1 на границю Z=0нормально падає поздовжня Р₁ монохроматична хвиля

,

В результаті відбиття – заломлення на границі Z=0 виникає відбита P₁₁ і заломлена Р₁₂ поздовжні хвилі (рисунок 5.1). Для потенціалів відбитої і заломленої хвилі маємо представлення

(5.11)

де невідомими є амплітуди.

Формула (5.11) виписана з таким розрахунком, щоб потенціали задовольняли своєму хвильовому рівнянню і щоб плоскі хвилі, що збуджувалися на границі розділу, розповсюджувалися би в бік від цієї границі. Цього вимагає рахунок умов випромінювання, яке при коливаннях, які встановилися, замінюють нульові початкові данні.

Потенціали мають також задовольняти граничним умовам, тільки в тому випадку рішення задачі будекоректним (єдиним). Граничні умови, які вимагають неперервності векторів 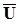і при переході через границю розділу Z=0 на підставі (5.1), (5.2), (5.8) зaписується у такому вигляді

, (5.12)

(5.13)

Підставляючи (5.11) і маючи Z=0, отримаємо

(5.14)

(5.15)

(5.16)

З врахуванням (5.14) рівність (5.16) матиме вигляд

З цього виразу легко знайти відношення А₁/А₀, тобто коефіцієнт відбиття. Виражаючи його через , отримаємо

або

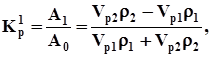(5.17)

де

Для визначення коефіцієнта проходження (заломлення) підставимо в (5.16) значення А₁з (5.15). Після перетворення, позначаючи А₂/А₀ через , отримаємо

(5.18)

А₀, А₁ і А₂ – амплітуди потенціалів відповідно падаючої, відбитої та заломленої хвиль. Тому коефіцієнти і є коефіцієнтами відбиття-заломлення по відношенню до потенціалів. Нас же цікавлять коефіцієнти відбиття – заломлення по відношенню до зміщень. Знайдемо ці коефіцієнти, позначивши їх через і .

Потенціал падаючої хвилі

Тому вектор зміщення 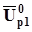падаючої хвилі на підставі (5.3) буде

(5.19)

Відповідно для векторів зміщення відбитої 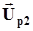заломленої хвиль, враховуючи (5.11), отримаємо

(5.20)

Позначимо амплітуди зміщень падаючої, відбитої і заломленої хвиль відповідно через U₀, U₁, U₂, тоді, беручи до уваги (5.19) і (5.20),

Звідси маємо

(5.21)

(5.22)

Підставляючи в (5.21) і (5.22) і з (5.17) і (5.18),остаточно отримаємо

(5.23)

(5.24)

З рівнянь що визначають коефіцієнти відбиття –заломлення, випливає ряд важливих наслідків. З (5.23) видно, що відбита хвиля з’являється завжди, якщо

Добуток густини середовища і швидкості розповсюдження хвилі в середовищі називають хвильовим опором (або акустичною жорсткістю) середовища. Відбиття хвилі відбувається на границі розділу хвильових опорів, заломлення – на границі розділу швидкостей, коли

Границі розділу хвильових опорів називаються відбиваючими границями, а границі розділу швидкостей – швидкісними границями. Оскільки густини гірських порід змінюються в значно більших границях, чим швидкості в них, швидкісні та відбиті границі зазвичай співпадають.

При нахиленому падінні на плоску границю складові вектора напруження (5.6) породжують складові вектора зміщення (5.7) над і під границею середовища. Причому, при падінні плоскої хвилі утворюється чотири вторинних хвилі: монотипні (по поляризації) відбита і заломлена хвилі та обмінні відбита та заломлені хвилі.

Наприклад, при падінні на границю Р хвилі під кутом a_Р утворюється: відбита РР хвиля під кутом a_Р, обмінна PS хвиля під кутом a _S, заломлена РР хвиля під кутом b_Р та заломлена обмінна хвиля PS під кутом b _S (рисунок 5.2).

Рисунок 5.2 – Нахилене падіння плоскої хвилі на границю двох середовищ

Співвідношення між кутами падіння та швидкостями розповсюдження пружних хвиль регламентується законом Снеліуса:

(5.25)

З цього закону, зокрема, випливає, що кут відбиття монотипної хвилі дорівнює куту падіння.

Швидкість, з якою точка перетину фронту хвилі з границею ковзає вздовж останньої, є позірною швидкістю і визначається законом Бендорфа:

. (5.26)

Ці два закони мають велике значення в геометричній сейсміці.

Поиск по сайту: