АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Хвильові рівняння з дисипативним членом

Читайте также:
  1. Бюджетні обмеження споживача, бюджетне рівняння та фактори впливу на бюджетну лінію.
  2. Геометричний зміст похідної. Рівняння дотичної.
  3. Грошовий обіг та його закони. Рівняння грошової та товарної мас (рівняння Ірвена Фішера). Грошові агрегати.
  4. Загальне рівняння фотосинтезу та походження кисню
  5. Змістовний модуль 6.2. «Рівняння, їх системи і сукупності.».
  6. Знаходження параметів лінійного рівняння регресії методом найменших квадратів
  7. Каждый парламентарий обязан быть членом хотя бы одной комис-
  8. КОМПЛЕКСНІ ХВИЛЬОВІ РІВНЯННЯ
  9. Лінійна кореляція і рівняння лінійної регресії
  10. Малюнок № 6.1. Графік рівняння кола.
  11. Моделі состава, відчепу і вагона. Диференціальне рівняння скочування відчепів з гірки
  12. Найбільш просте рівняння стану системи – рівняння стану для 1 моль ідеального газу

Для розгляду хвиль в реальних середовищах поставимо наступні умови:

1. Будемо рахувати, що рішенням хвильового рівняння є функція зміщення

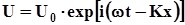, (6.1)

де w - частота коливань, К - комплексне хвильове число* .У свою чергу К = k - іa, де k - дійсна частина хвильового числа, a - коефіцієнт затухання, і – уявна одиниця.

2. Дисперсійне співвідношення для даної моделі хвильового рівняння повинно бути дійсним.

3. Коефіцієнт хвильового рівняння перед другою просторовою похідною дорівнює добутку групової та фазової швидкостей: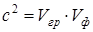

Ці три умови є достатньо природними. Так для ідеально пружного середовища маємо хвильове рівняння

, (6.2)

а дисперсійне співвідношення для (6.2)

. (6.3)

По умові 2 уявна частина (6.3) дорівнює нулю, звідки коефіцієнт затухання дорівнює нулю, а фазова та групова швидкість між собою рівні 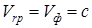, що відповідає умові 3. Як і слід було очікувати, затухання та дисперсія хвиль у ідеально пружному середовищі відсутні.

 

 

 
 


*Тут і далі аргументи поля зміщень U(t,х) для спрощення

опускаємо.

Одним з найпростіших хвильових рівнянь для диспергуючих середовищ є рівняння Клейна-Гордона

. (6.4)


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)