 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Найбільш просте рівняння стану системи – рівняння стану для 1 моль ідеального газу
рv = RT (І.1.2)
Або, якщо розглядається n моль газу, то
рV = nRT (І.1.3)
З позицій математики стверджування незалежності зміни параметрів від шляху, по якому відбувається зміна, еквівалентне такому положенню: безкінечно мала зміна параметру системи є повним диференціалом. Дійсно, будь-який параметр системи можна, щонайменше в загальному вигляді, подати як функцію інших параметрів. Наприклад, для мольного об’єму
v = f (р, T) (І.1.4)
Продиференціювавши це рівняння, знаходимо повний диференціал функції двох змінних:
(І.1.5)
При кінечній зміні системи, наприклад, при переході зі стану 1 в стан 2, повна зміна параметру буде складатись із малих змін на безкінечно малих ділянках шляху, по якому відбувається зміна. Іншими словами, повну зміну параметру можна подати інтегралом:
(І.1.6)
Згідно з математичним аналізом інтеграл від повного диференціалу не залежить від шляху інтегрування. Таким чином, твердження про незалежність зміни параметрів від шляху, по якому відбуваються зміни в системі, можна замінити еквівалентним – зміна параметрів системи є повним диференціалом. Справедливим буде і зворотний висновок, а саме, якщо зміна якої-небудь величини не залежить від шляху перетворення системи, то ця величина є параметром стану системи.
При v = const
dv = 0 (1.1.7)
Тоді рівняння (І.1.5) запишеться у вигляді
(І.1.8)
Ділимо це рівняння на величину dT і прийнявши, що dр/dT є частинною похідною при умові незмінності стану системи, запишемо рівняння (І.1.8) у такому вигляді:
(І.1.9)
Або його можна записати інакше:
(I.1.10)
Одержане таким чином рівняння (І.1.10) є рівнянням стану системи в диференційній формі. Аналогічні вирази можуть бути одержані для будь-яких змінних, що зв’язані функціональною залежністю, тобто рівняння (І.1.10) має загальний характер. Такі рівняння дають можливість встановити зв’язок між коефіцієнтами об’ємного розширення системи a при сталому тиску, ізотермічним коефіцієнтом її стискування b і термічним коефіцієнтом тиску g. Покажемо це так:
(І.1.11)
де Vo – об’єм фази при температурі То;
(І.1.12)
де Vo´ – об’єм фази при стандартному тиску ро і будь-якій заданій для ізотермічного стискування, температурі Т;
(І.1.13)
де ро – тиск фази при стандартній температурі То.
Коефіцієнти a, b і g називаються термічнимикоефіцієнтами.
Користуючись вище приведеними співвідношеннями і рівнянням (І.1.9), та при умові, що Т = Т0, а 
одержуємо шукану залежність у вигляді
a = g×b× ро (І.1.14)
За цим рівнянням обчислюють один із цих коефіцієнтів, якщо два інших знайдені експериментальним шляхом
Наближено рівняння (І.1.2) можна застосовувати і до реальних газів. Для таких газів максимальне відхилення поведінки від властивостей ідеальних газів спостерігається при високих тисках і низьких температурах. При цих умовах об’єм системи стає відносно малим і власний об’єм молекул уже складає помітну частку загального об’єму. Окрім цього, коли молекули знаходяться на близьких відстанях одна від одної, експериментально виміряний тиск виявляється значно меншим від розрахованого за вище згаданим рівнянням. Причиною відхилення є сили міжмолекулярного притягання.
Таким чином, рівняння (І.1.2) можна застосовувати для реальних газів лише тоді, коли тиск не дуже високий і температура не дуже низька і розв’язувати з певною похибкою, багато задач фізичної хімії. Наприклад, рівняння (І.1.3) записане у такому вигляді
(І.1.15)
часто використовується для визначення мольної маси (метод В. Майєра). Отже, без перебільшення можна сказати, що вся класична термодинаміка і в значній мірі фізична хімія в своїх застосуваннях пов’язана з рівнянням стану ідеального газу.
Функціональні залежності параметрів стану системи зображуються графіками у вигляді так званих ізотерм. Прикладом може бути залежність об’єму газу від тиску при сталій температурі:
V = f (р) (T = const) (І.1.16)
Для ідеального газу залежність
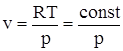(І.1.17)
є рівностороння гіпербола, положення якої залежить від температури.
На рис. 1 наведені дві ізотерми ідеального газу при 273 і 373 К. На ньому ж показані експериментальні (реальні) ізотерми азоту. Пунктирні криві, що відповідають азоту, помітно відхиляються від ідеальних ізотерм в області високих тисків, де стискуваність реального газу менша, ніж ідеального, і тиск зі зменшенням об’єму зростає швидше. Зі зниженням тиску суцільні і пунктирні криві на рисунку даного масштабу зливаються, тобто в міру зменшення тиску (підвищення температури) властивості реального газу наближаються до властивостей ідеального.
Відхилення поводження реального газу від ідеального збільшується також при зниженні температури. На рис. 2 наведено ряд ізотерм для карбон диоксиду. Як видно, при температурах нижче 31,3оС на ізотермах з’являються горизонтальні ділянки. Вони відповідають ділянкам співіснування пари і рідини (двохфазна система). На рисунку пунктирною кривою подана так звана критична ізотерма, тобто ізотерма при критичній температурі. Вище цієї ізотерми газ не можна перевести в рідину ніяким стискуванням.
Якщо стискувати один моль газу, стан якого визначається точкою а, при сталій температурі (ізотерма при температурі 21,5оС), то спочатку зменшення об’єму супроводжується підвищенням тиску, але, починаючи зі стану, що відповідає точці b, подальше зменшення об’єму відбувається при сталому тиску. При цій температурі речовина є не газом, а парою, яка в точці b стає насиченою. На протязі прямої bс відбувається конденсація пари. Об’єм, що відповідає точці b, є мольним об’ємом насиченої пари V n а в точці с – мольним об’ємом рідини V р.
Різка зміна тиску від точки с пов’язана з малою стискуваністю рідини. При більш високих температурах спостерігається аналогічна крива, проте її горизонтальна ділянка, тобто область співіснування рідини і пари, скорочується і при критичній температурі зникає зовсім. На рисунку область двохфазної системи заштрихована (асКbr). Точка, що лежить на вершині області існування пари і рідини, називається критичноюточкою. В системі р-V їй відповідають координати – критичний об’єм Vкр і критичний тиск ркр і, які поряд з критичною температурою, є величинами, що характеризують речовину. Критичні величини для відповідних речовин можна знайти в довідниковій літературі.
Таким чином, шлях abdch перетворення пари в рідину відбувається через гетерогенну, тобто неоднорідну область, де система розділяється на дві фази – рідку і пароподібну. Проте, якщо йти шляхом agfeh, то газ можна перевести в рідину в обхід гетерогенної області, без розділення системи на дві фази.
Рівняння (І. 1.15), як це витікає із вищезазначеного не відбиває поводження реальних газів і особливо при температурах нижче критичних. У зв’язку з цим було запропоновано багато інших рівнянь, що зв’язують змінні р, V, Т і точніше передають реальні залежності між ними. Найбільш відомим з таких рівнянь є рівняння Ван-дер-Ваальса, яке враховує власний об’єм молекул, яким в кінетичній теорії ідеального газу нехтують, а також сили взаємодії між молекулами, що залежать від відстані між ними. Якщо уявити молекули газу у вигляді кулі, що не стискуються, і прийняти їх діаметр рівним d, то, як видно з рис. 3, навколо кожної молекули існує,,заборонений об’єм“ радіусом d, в середину якого не може проникнути центр іншої молекули. На один моль речовини цей об’єм повинен складати 4/3× N Ap d 3, але оскільки в зіткненні беруть участь дві молекули, то об’єм, що недоступний для вільного руху молекул, слід вважати рівним половині вказаного. Тож для вільного руху молекул залишається об’єм
v – b,
де v – мольний об’єм газу, а b = 4(1/6 × N Ap d 3), тобто збільшений у чотири рази власний об’єм молекул.
Взаємне притягання молекул газу обумовлене дією сил Ван-дер-Ваальса. Ці сили, викликаючи зменшення об’єму газу, діють на нього як деякий додатковий до зовнішнього тиск, який називають внутрішнімтиском. Цей тиск зростає пропорційно квадрату густини, тобто р = аr 2, де а – величина стала для даного газу. Густина газу обернено пропорційна його мольному об’єму:
, звідки 
.
Тоді рівняння Ван-дер-Ваальса матиме вигляд
(І.1.18)
або для n моль речовини
(І.1.19)
Сталі величини а і b для багатьох речовин визначені. На рис. 2 пунктиром наведена крива для температури 31,3ºС, що обчислена за цими константами для карбон диоксиду. Перемноживши в рівнянні (І.1.18) вираз в дужках та розділивши його на р і помноживши на v2, розташовуємо члени в порядку зменшення ступеня v, отримуємо
(І.1.20)
При температурі нижче критичної це кубічне рівняння має три корені, тобто кожному значенню р відповідають три значення V. Ці об’єми визначаються точками перетину b, d, c на кривій abcdh з горизонтальною лінією, що відповідає сталому тиску (рис. 2). Проте із цих трьох коренів дійсними є лише два, а саме ті, що відповідають точкам b i c і фізично реальні. Третій корінь (точка d) фізично не реальний і лежить на вітці кривої, що відповідає неможливому процесу, пов’язаному зі збільшенням об’єму при збільшенні тиску. (Однак, деякі ділянки хвилеподібної кривої фізично можна реалізувати).
Значення констант у рівнянні Ван-дер-Ваальса можна розрахувати із критичних констант газу. Як видно з рис. 2, критична точка є точкою перегину на ізотермі, що відповідає критичній температурі; тож
(І.1.21)
Для критичної температури рівняння Ван-дер-Ваальса можна записати
(І.1.22)
Продиференціювавши це рівняння за мольним об’ємом, одержуємо:
(І.1.23)
(І.1.24)
У критичній точці обидві похідні рівні нулю, а v і р заміняються на vкр і ркр.
Рівняння (І.1.22), (І.1.23) і (І.1.24) можна розв’язати сумісно. При цьому одержуємо
(І.1.25)
Критичні константи можна виразити через константи рівняння Ван-дер-Ваальса:
(І.1.26)
Варте уваги рівняння Ван-дер-Ваальса в так званій приведеній формі. Якщо в рівнянні (І.1.9) сталі а, b і R замінити виразами із (І.1.25), то одержимо рівняння:
(І.1.27)
Якщо одержане рівняння одночасно поділити на ркр×vкр і помножити на 3, то рівняння (І.1.27) можна подати у вигляді функцій таких співвідношень:
(І.1.28)
які називаються відповідно приведенимтиском, приведенимоб’ємом і приведеноютемпературою. А рівняння
(І.1.29)
називається приведеним рівнянням стану Ван-дер-Ваальса.
Оцінити з певною точністю термодинамічний стан системи якимось одним рівнянням не вдається. Тому було запропоновано багато різних рівнянь для ряду окремих випадків (понад 150). Проте, для того, щоб достатньо точно зображати експериментальні дані в широкому інтервалі зміни умов системи, потрібно велике число констант. Досить корисним вважають рівняння стану з віріальними коефіцієнтами:
рv = RT(1 + B /v + C /v2 + D /v3 +...) (І.1.30)
Рівняння (І.1.30) можна записати в дещо іншому вигляді:
р×v = RT(1 + b р + c р2 + d р3...) (І.1.31)
У цих рівняннях B, C, D... або b, c, d... другий, третій, четвертий і т. д. віріальні коефіцієнти.
Ці коефіцієнти залежать лише від температури: їх обчислюють, використовуючи методи статистичної термодинаміки. Вони відбивають парні (B), потрійні (C), чи взаємодії чотирьох (D) і т. д. частинок газу. Для розрахунку слугує співвідношення, що встановлює зв’язок між енергією взаємодії молекул, відстанню між ними і їх розташування. Встановлено, що для невисоких тисків коефіцієнт B більший за C, а останній зростає з підвищенням тиску і т. д.
У випадку низького тиску (р < ркр) можна обмежитись використанням другого віріального коефіцієнту. Тобто користуватись рівнянням:
р×v = RT(1 + B /v), (І.1.32)
що враховує лише парні взаємодії. Це рівняння застосовують досить часто.
При врахуванні не лише В, а і С рівняння стану дає задовільні результати, аж до ркр (при Т > Ткр).
Віріальне рівняння стану, що є єдиним теоретично обгрунтованим рівнянням стану реальних газів, все ж не знаходить належного застосування. Це обумовлено як складністю визначення його коефіцієнтів, так і тим, що з невеликою похибкою може бути визначений лише другий віріальний коефіцієнт.
Не менш складним є питання про рівняння стану системи, коли мова йде про суміш реальних газів. І. Р. Кричевський і Я. С. Казарновський для таких систем запропонували рівняння такого виду
р = ро1× х 1+ ро2× х 2 + j×(v, x2), (I.1.33)
де j - функція, яка залежить лише від температури.
Функція j тим більша, чим більша різниця ро1 - ро2, зміна знаку j×(v, x2) співпадає зі зміною знаку для ро1 - ро2 . Тому припускають, що ці величини пропорційні одна одній, і тоді попереднє рівняння приймає вигляд:
р = ро1× х 1+ ро2× х 2 + а × х 1× х 2(ро1 – ро2), (І.1.34)
де ро1 і ро2 – тиски компонентів при мольних об’ємах, рівних мольному об’єму газової суміші; а – константа, що характерна для даної суміші.
Це рівняння відрізняється високою точністю як для низьких, так і для високих тисків. Розрахунок за ним вимагає небагато даних і значно спрощується, якщо суміш не містить полярних компонентів, оскільки константа а тоді не залежить від температури.
І. 2. Енергія, теплота і робота
Невід’ємною властивістю матерії є рух. Рух, як і сама матерія, є незнищуваним. Мірою руху матерії є енергія.
Під повною енергією системи розуміють суму кінетичної, потенціальної і внутрішньої енергії, що зображають рівнянням:
Е = Ек + Еп + U, (І.2.1)
де Ек – кінетична енергія руху всієї системи, Еп – потенціальна енергія всієї системи в полі тяжіння, U – внутрішня енергія системи, тобто та кінетична і потенціальна енергія, якою володіє вся сукупність частинок, що складають дану систему. Вона залежить від параметрів, що характеризують стан системи.
Внутрішню енергію системи можна виразити рівнянням:
U = Uк + Uп, (І.2.2)
де Uк – енергія руху частинок системи і Uп – енергія взаємодії частинок між собою.
Кінетична енергія частинок системи є сумою трьох складових: кінетичної енергії поступального руху частинок, кінетичної енергії їх обертового руху і кінетичної енергії коливного руху частинок:
Uк = Uк. пост. + Uк. об. + Uк. кол. (І.2.3)
В окремих випадках може бути таке, що повна енергія тіла або системи в цілому рівна її внутрішній енергії, тобто Е = U. Таке буває при Ек = 0, Еп = 0, тобто коли система знаходиться в спокої поза полем сил тяжіння.
Одне із основних положень термодинаміки полягає в тому, що в будь-якому конкретному процесі слід розрізняти дві форми переходу енергії із системи в навколишнє середовище або, навпаки, із навколишнього середовища в систему: обмін енергією через хаотичний тепловий рух частинок шляхом їх зіткнення або обмін енергією через,,організований“ макроскопічний рух частин системи під дією прикладеної сили.
Якщо дві системи з різною температурою не є ізольованими і приведені до контакту між собою, то між ними розпочинається теплообмін. Частинки в цих системах знаходяться в стані теплового хаотичного руху. Внаслідок зіткнень між частинками, що мають різну швидкість руху, відбувається зміна їх кінетичної енергії і, відповідно, вирівнюється температура. Мірою передачі енергії таким способом є теплота. Система може обмінюватись енергією з навколишнім середовищем у формі теплоти і без зіткнень молекул. Наприклад, вона може випромінювати або поглинати променеву енергію. В цьому випадку випромінювання або поглинання одиничного кванту енергії аналогічне одиничному зіткненню частинок.
Друга форма обміну енергією між системами чи між системами і навколишнім середовищем називається роботою. Під роботою, що здійснюється внутрішніми силами системи проти зовнішніх сил чи, навпаки, зовнішніми силами проти внутрішніх, розуміють процес організованого макроскопічного переміщення частин систем однієї відносно іншої або взаємодії між системою і зовнішнім середовищем, внаслідок чого долаються зовнішні сили, що порушили рівновагу в системі. Робота виражається сумою добутку діючих на систему сил на відповідний шлях (тиску на зміну об’єму, поверхневого натягу на зміну поверхні і т. д.). Якщо єдиною діючою силою на систему є зовнішній тиск, то багаточлен, що виражає роботу, перетворюється на одночлен. Для елементарного процесу, цей одночлен приймає вигляд pdV. Домовимося, якщо про це окремо не застерігається, розглядати системи, що піддаються дії лише тиску. Майже не будемо торкатись тих випадків, коли робота не може бути виражена через ∫ pdV.
В термодинаміці прийнято вважати позитивною роботу, що виконується системою над середовищем (наприклад при розширенні газу, пароутворенні, дисоціації, в хімічних реакціях між речовинами, коли продуктами реакції є гази, або в реакціях з утворенням більшої кількості газуватих речовин, ніж їх вступило в реакцію). У випадках, коли робота над системою виконується зовнішніми силами (наприклад, при стискуванні газів), її вважають негативною.
Енергія, що передається одним тілом іншому при їх взаємодії і залежать лише від температури цих тіл, і не пов’язана з перенесенням речовини від одного тіла до іншого, називається теплотою процесу. Виділення або поглинання теплоти (Q) є наслідком порушення термічної рівноваги між системою і зовнішнім середовищем. Енергію, що підводиться до системи у формі теплоти, в термодинаміці прийнято вважати позитивною, а та, що віддається нею – негативною. Так, тепловий ефект екзотермічної хімічної реакції є негативним, а ендотермічної – позитивним. Процес, при якому система не одержує теплоти ззовні і не віддає її, називається адіабатним.
Таким чином, ні теплота, ні робота не є видами чи формами енергії. Це форми обміну енергією системи з навколишнім середовищем. Не мають сенсу висновки,,теплова енергія“,,,запас теплоти“,,,запас роботи“. В системі є лише запас енергії (тобто кінетичної і потенціальної енергії частинок, що її складають). Енергія системи пов’язана з її станом. Терміни,,теплота“ і,,робота“ втрачають зміст, поки система знаходиться в якомусь певному стані. Ці терміни не застосовуються до,,стану системи“ як такого, а лише до системи, яка переходить із одного стану в інший. І тоді вони визначають форми переходу енергії із системи в навколишнє середовище або навпаки.
Наведений аналіз понять,,теплоти“ і,,роботи“ дозволяє зробити висновок, що в певному відношенні ці дві форми обміну енергією нерівноцінні. Відношення кількості роботи до кількості теплоти буде залишатись незмінним, коли відбуваються взаємоперетворення лише роботи і теплоти, тобто коли теплота (робота) не перетворюється крім роботи (теплоти) в інші форми руху. Лише в цьому випадку відношення кількості роботи до кількості теплоти залишається незмінним.
Проте, неможливо реалізувати жоден процес, в якому обмін енергією здійснювався б лише в організованих макроскопічних масштабах, тобто лише у формі роботи. Тепловий рух частинок існує в будь-якій системі, і тому, поруч із виконуваною роботою, неминучий обмін енергією також і в формі теплоти.
Розглядаючи в загальному вигляді процес обміну енергією між системою і навколишнім середовищем, слід врахувати, що енергія системи може змінюватись ще і третім способом (крім теплоти і роботи), а саме внаслідок переходу в систему з навколишнього середовища або, навпаки, деякої кількості речовини. Дійсно, обмін речовиною веде до того, що кількість молекул того чи іншого виду в системі змінюється, тож змінюється сума кінетичної і потенціальної енергії частинок в системі, тобто змінюється загальний запас енергії в системі.
Поиск по сайту: