Геометрическая оптика. Разрешающая сила оптических систем

При падении света на границу раздела двух прозрачных веществ падающий луч разделяется на два – отраженный и преломленный. Направления этих лучей определяются законами отражения и преломления света.

Закон отражения света.

Отраженный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной в точке падения. Угол падения равен углу отражения:

a = g (4.3.15)

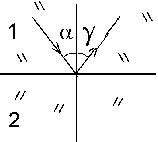
Закон преломления света.

Преломленный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной в точке падения. Отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных веществ:

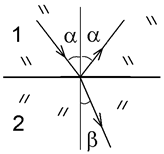sina / sinb = n ₂/ n ₁. (4.3.16)

Здесь n ₁ и n ₂ – абсолютные показатели преломления первой и второй сред относительно.

Вещество с большим показателем преломления называют оптически более плотным.

При переходе света из оптически более плотной среды в оптически менее плотную луч света будет удаляться от нормали к поверхности. Увеличение угла падения a сопровождается более быстрым ростом угла преломления b и по достижении углом a некоторого предельного значения

a_пред = arcsin(n ₂ /n ₁), (4.3.17)

угол b становится прямым (b = p /2).

При углах падения, заключенных в пределах от a_пред до p /2, свет полностью отражается от границы сред. Это явление носит название полного внутреннего отражения, а выражение (4.3.17) называется предельным углом полного внутреннего отражения.

Прозрачное тело, ограниченное, к примеру, двумя сферическими или сферической и плоской поверхностями, называется линзой. Точка линзы, через которую любой луч проходит не изменяя своего направления, называется главным оптическим центром О линзы. Прямая FF, проходящая через центры О ₁ и О ₂ сферических поверхностей, называется главной оптической осью. Остальные оси, проходящие через оптический центр линзы, называют побочными, а плоскости, перпендикулярные к главной оптической оси, и проходящие через фокусы – фокальными плоскостями линзы. Любая прямая АВ, проходящая через оптический центр линзы, называется побочной осью линзы.

M

А

F F

O₁ O O₂

N

В

Линзы, превращающие падающий на них параллельный пучок лучей в пучок сходящихся лучей, называется собирающими.

Линзы, превращающие падающий на них параллельный пучок лучей в пучок расходящихся лучей, называется рассеивающими. Схематические изображения собирающей и рассеивающей линз изображены на рисунке ниже:

Пучок лучей, параллельных главной оптической оси, после преломления в линзе сходится в главном фокусе F. Для собирающей линзы главный фокус является действительным, для рассеивающей – мнимым. Каждая линза имеет два фокуса: передний и задний. Плоскость MN, проведенная через главный фокус перпендикулярно главной оптической оси, называется фокальной. Каждый из лучей, параллельных оптической оси, после преломления в линзе проходит через одну и ту же точку, лежащую на фокальной плоскости линзы (в параксиальном приближении).

Для построения изображений в линзах из всего пучка лучей, падающих на линзу, удобно использовать следующие лучи:

1) луч, параллельный главной оптической оси, после преломления проходит через правый главный фокус;

2) луч, проходящий через левый главный фокус, после преломления проходит параллельно главной оптической оси;

3) луч, проходящий через оптический центр линзы, после преломления проходит по тому же направлению (справедливо только для тонкой линзы).

Формула тонкой линзы:

, (4.3.18)

где d – расстояние от предмета до линзы, f – расстояние от линзы до изображения, F – фокусное расстояние линзы. В формуле (4.3.18) берется знак «плюс», если изображение является действительным, «минус», если мнимым. У собирающей линзы фокусное расстояние F > 0, у рассеивающей линзы F < 0.

Оптическая сила линзы D – это величина, обратная фокусному расстоянию линзы (n – показатель преломления среды):

D = n / F. (4.3.19)

Оптическая сила системы тонких прижатых друг к другу линз является суммой оптических сил этих линз:

D = D ₁ + D ₂ + D ₃ + … (4.3.20)

Линейное увеличение линзы – это отношение линейного размера изображения А ₁ В ₁ к линейному размеру предмета АВ.

Г = | А ₁ В ₁|/| АВ | = f/d. (4.3.21) Линейное увеличение оптической системы тонких линз – это произведение линейных увеличений каждой линзы в отдельности:

Г = Г ₁ Г ₂ Г ₃… (4.3.22)

Расстояние наилучшего зрения для человеческого глаза: L» 0,25 м.

Простейший микроскоп состоит из двух собирающих линз – объектива и окуляра.

Для определения разрешающей способности микроскопа Аббе предложил освещать объект когерентным излучением, в качестве объекта была выбрана дифракционная решетка с постоянной d.

Разрешающая способность микроскопа:

Z , (4.3.23)

где l – длина волны света, n – показатель преломления среды, в которой находится объект (u /2) – апертура (половина угла между крайними лучами, идущими от объекта к краям объектива).

Угловая дисперсия дифракционной решетки:

D = k /(dcosj), (4.3.24)

где k – порядок дифракции, d – постоянная дифракционной решетки, j – угол дифракции.

По критерию Рэлея два интерференционных пика интенсивности, еще можно увидеть раздельно, если минимум первого пика с длиной волны (l + D l)совпадает с максимумом второго пика в спектре k -того порядкас длиной волны l. Отсюда следует, что

l/Dl = kN, (4.3.25)

где отношение l / Dl называется разрешающей способностью дифракционной решетки, N – число штрихов дифракционной решетки.

Пример 9. Собирающая линза дает действительное, увеличенное в 2 раза изображение предмета. Определить фокусное расстояние линзы, если расстояние между линзой и изображением составляет 24 см. Построить изображение предмета в линзе.

Дано: Г = 2; f = 24 см = 0,24 м.

Найти: F.

Решение.

A

A ₁

2 F B F F 2 F B ₁

d f

Для построения изображения верхней точки А предмета АВ рассмотрим два луча. Первый луч, идущий параллельно главной оптической оси, преломившись, пройдет через главный фокус линзы; второй, идущий через главный оптический центр линзы, не изменит своего направления. Точка пересечения А ₁ этих лучей является действительным изображением точки А. Опустив из точки А ₁ перпендикуляр на главную оптическую ось, получим действительное, увеличенное и перевернутое изображение А ₁ В ₁ предмета АВ. Для нахождения фокусного расстояния воспользуемся формулой тонкой линзы (4.3.18), откуда выразим фокусное расстояние F:

F = df /(d+f). (4.3.26)

Линейное увеличение линзы найдем из формулы (4.3.21):

Г = f / d, откуда d = f / Г. (4.3.27)

Подставив соотношение (4.3.27) в (4.3.26), найдем

F = f /(Г+ 1) = 0,24/(2+1) = 8×10^{-2 м}.

Ответ: F = 8×10^{-2 м.}

Пример 10. Какое увеличение дает лупа, если ее оптическая сила равна 16 дптр? Построить изображение предмета в лупе.

Дано: D = 16 дптр.

Найти: Г.

Решение. Если не учитывать расстояние между глазом и линзой, то увеличение, даваемое лупой с фокусным расстоянием F, как следует из (4.3.21), будет равно

Г = f/d.

В частном случае, когда предмет расположен так, что его изображение получается на расстоянии наилучшего зрения нормального глаза(L = 0,25 м), должно быть f = L, поэтому увеличение, даваемое лупой,

Г = L / F = LD,

где F – фокусное расстояние лупы, причем D = 1/ F, как следует из (4.3.19).

Следовательно, Г = 0,25×16 = 4.

A ₁

A

В ₁ F B O F

Чтобы рассмотреть предмет через лупу, его располагают между лупой и ее фокусом. Для построения изображения точки А этого предмета используем два луча, исходящие из нее: один, параллельный главной оптической оси, после преломления проходит через фокус; другой, проходящий через главный оптический центр линзы, не изменит своего направления. Изображение А ₁ точки А получится в точке пересечения продолжения лучей. Аналогично получаем изображение В ₁ точки В. Следовательно, изображение А ₁ В ₁ предмета АВ мнимое, увеличенное и прямое.

Пример 11. Микроскоп состоит из объектива и окуляра, расстояние между главными фокусами которых 18 см. Найти увеличение, даваемое микроскопом, если фокусные расстояния объектива и окуляра соответственно равны 2 и 40 мм. Построить изображение предмета.

Дано: l = 18 см = 0,18 м, F ₁ = 2 мм = 2×10^{-3 м,} F ₂= 40 мм = 4×10^{-3 м.}

Поиск по сайту: