Электромагнитная индукция. ЭДС индукции и самоиндукции

Пусть некоторый замкнутый контур Г находится в неоднородном магнитном поле. Контур Г ограничивает поверхность S, как показано на рисунке ниже. Поток индукции F магнитного поля через поверхность S – это величина, которая определяется выражением

F = ò BdScosa, (3.3.16)

где B – магнитная индукция, a – угол между вектором магнитной индукции и нормалью к площадке поверхности dS, которую магнитное поле пронизывает.

a

dS

Если поверхность S, ограниченная контуром Г, плоская и имеет, к примеру, форму круга или квадрата, то интеграл (3.3.16) по этой поверхности превращается в выражение

F = ò BdScosa = BScosa, (3.3.17)

где S = pR ², если поверхность – круг радиуса R,

S = а ², если поверхность – квадрат со стороной а.

Закон электромагнитной индукции Фарадея: при изменении магнитного потока F через поверхность S, опирающуюся на замкнутый проводящий контур Г, в нем возникает ЭДС электромагнитной индукции:

. (3.3.18)

Поток F может изменяться вследствие следующих причин:

1. Изменяется площадь S поверхности, ограниченной контуром Г.

2. Изменяется угол a между вектором магнитной индукции и нормалью к площадке поверхности dS, которую магнитное поле пронизывает (это может происходить, когда контур вращается в магнитном поле).

3. Изменяется индукция магнитного поля .

Протекая по замкнутому проводнику, ток I создает магнитное поле и магнитный поток, пронизывающий площадь, охватываемую проводником. Величина такого магнитного потока пропорциональна величине тока в нем:

F = L×I. (3.3.19)

Здесь L – индуктивность контура.

В случае если протекающий по контуру Г ток начинает изменяться с течением времени, в этом контуре возникает ЭДС самоиндукции

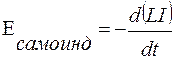, (3.3.20)

а явление носит название самоиндукции.

Знак «–» в формулах (3.3.18) и (3.3.20) означает, что при изменении магнитного потока сквозь замкнутый контур в нем возникает такая ЭДС, которая стремится уменьшить изменение потока. Это правило Ленца.

Пример 28. Квадратный проводящий контур со стороной

а = 1 см пронизывает однородное магнитное поле под углом

a = 30° к вектору нормали контура. Найти модуль ЭДС индукции в контуре в момент времени t = 2с, если А = D = 1 Тл, t = 1с,

B (t) = A (t / t) + D (t / t)⁴.

Дано: а = 1 см = 0,01 м.

a = 30°,

А = D = 1 Тл,

t = 1с,

t = 2с,

B (t) = A (t / t) + D (t / t)⁴.

Найти: ½ Е_инд ½.

Решение. Запишем исходные формулы для модуля ЭДС индукции (это формулы (3.3.17) и (3.3.18)):

F = ò BdScosa = BScosa,

.

По условию задачи контур квадратный, его площадь будем вычислять по формуле:

S = а ².

Подставим в (3.3.18) закон изменения магнитной индукции В от времени, данный в условии задачи, и продифференцируем по времени:

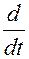= [ A (t / t) + D (t / t)⁴] Scosa = (А / t + 4 Dt ³/ t ⁴) Scosa =

= (А / t + 4 Dt ³/ t ⁴) a ² cosa = 2,86×10^–3 В.

Ответ: 2,86×10^–3 В.

Замечание. Если в условии задачи сказано, что проводящий контур пронизывает однородное магнитное поле под углом a к плоскости контура, мы то имеем следующую картину:

b

a

Поскольку в формулах (3.3.16)–(3.3.17) угол a – это угол между нормалью к контуру и вектором магнитной индукции, то, как следует из нашего рисунка, в (3.3.16)–(3.3.17) мы должны подставлять угол b = 90° – a.

Пример 29. По проводящему контуру индуктивностью

L = 1 Гн течет ток, изменяющийся со временем по закону

I (t) = B (t / t)². Найти момент времени, в который величина ЭДС самоиндукции в контуре составляет 2 В, если В = 1А, t = 1с.

Дано: I (t) = B (t / t)²,

Е_{самоинд} = 2 В,

В = 1А,

t = 1с,

L = 1 Гн,

Найти: t.

Решение. Время t выразим из (3.3.20):

.

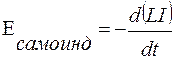Поскольку в условии задачи речь идет о модуле ЭДС самоиндукции, то знак «–» в (3.3.20) сменится на обратный. Подставим в (3.3.20) закон изменения силы тока, данный в условии задачи и продифференцируем по времени:

[ L (B (t / t)²)] = 2 LBt/t ²,

откуда выразим время t:

t = (½ Е_{самоинд} ½ t ²)/(2 LB) = 1 с.

Ответ: 1 с.

Поиск по сайту: