 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Основное уравнение динамики поступательного движения материальной точки. Импульс. Закон сохранения импульса
Импульс материальной точки, имеющей массу m и скорость 
– это вектор, равный произведению массы на скорость:
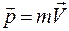. (1.3.38)
Введем понятие замкнутой системы как совокупности материальных тел, включая и точечные массы, взаимодействующие друг с другом и не взаимодействующие с окружающими замкнутую систему телами. Для замкнутой системы существует несколько величин, связанных со скоростями входящих в нее тел, которые не изменяются с течением времени. Такие величины называют сохраняющимися.
Одной из сохраняющихся величин является полный импульс замкнутой системы, равный векторной сумме импульсов образующих ее точечных масс:
,
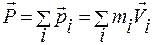где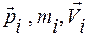 
– импульс, масса и скорость i -той материальной точки, а суммирование ведется по всем точкам замкнутой системы.
Таким образом, система называется замкнутой, если все внешние силы, действующие на систему, уравновешиваются (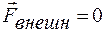
). Тогда имеет место закон сохранения импульса:
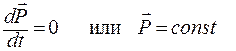, (1.3.39)
то есть
Полный импульс замкнутой системы сохраняется.
Если, например, 
, то есть, сохраняется только проекция импульса на соответствующую ось.
Если частица взаимодействует с окружающими телами, то ее импульс будет изменяться с течением времени. Мерой такого изменения и, следовательно, характеристикой взаимодействия является сила, определяемая как
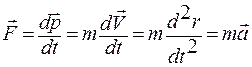. (1.3.40)
Выражение (1.3.40) являетс я основным уравнением динамики поступательного движения частицы и носит название второго закона Ньютона.
Рассмотрим примеры решения задач.
Пример 14. Импульс материальной точки массы 1 кг изменяется со временем по закону 
. Найти величину ускорения материальной точки через 1 секунду после начала движения. А = 2 кг×м/с4, В = 3 кг×м/с2, С = 2 кг×м/с.
Дано: ;
А = 2 кг×м/с4, В = 3 кг×м/с2, С = 2 кг×м/с;
m = 1 кг.
Найти: а.
Решение. Величину ускорения частицы найдем из второго закона Ньютона (1.3.40):
а = F / m,
причем модуль силы, аналогично (1.3.23), получим так:
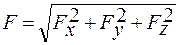, (1.3.41)
где Fx, Fy, Fz – проекции силы на оси координат, которые согласно (7.3), равны соответственно:
Fx = dpx / dt, Fy = dpy / dt, Fz = dpz / dt. (1.3.42)
По условию задачи px = Аt 3, py = Bt, pz = C.
Тогда, согласно (7.5), имеем для проекций силы на оси координат:
Fx = dpx / dt = d (Аt 3)/ dt = 3 At 2 = 6 (Н),
Fy = dpy / dt = d (Bt)/ dt = B = 3 (Н),
Fz = dpz / dt = d (C)/ dt = 0.
Подставим полученные значения проекций силы в (1.3.41), а затем в (1.3.40):
F = (62 + 32)1/2 = 6,7 (Н).
а = 6,7 (м/с2).
Ответ: 6,7 м/с2.
Пример 15. Два шара массами 2 кг и 3 кг движутся по плоскости без трения и проскальзывания со скоростями 4 м/с и 2 м/с соответственно. После неупругого удара найти скорость шаров, если а) первый шар догоняет второй; б) шары движутся навстречу друг другу.
Дано: m 1 = 2 кг, m 2 = 3 кг,
v 1 = 4 м/с, v 2 = 2 м/с.
Найти: u 1, u 2.
Решение. а) Рассмотрим случай, когда шары движутся в одном направлении.
При неупругом ударе тела движутся вместе со скоростью, которую мы обозначим u.
u 1 
u 2 u
m 1 m 2 m 1+ m 2 x
до удара после удара
Направление оси О x выберем в направлении скоростей тел, как показано на рисунке. Система двух шаров является замкнутой по условию задачи, поэтому для нее будет выполняться закон сохранения импульса (1.3.39). Запишем его в проекции на ось О x:
m 1 u 1 + m 2 u 2 = (m 1+ m 2) u,
откуда выразим скорость системы после удара:
u = (m 1 u 1 + m 2 u 2)/(m 1+ m 2) = 2,8 (м/с).
б) Шары движутся навстречу друг другу:
u 1 u 2 u
m 1 m 2 m 1+ m 2 x
до удара после удара
Предположим, что после удара шары будут двигаться в направлении движения первого шара до соударения. Запишем закон сохранения импульса в проекции на ось О x:
m 1 u 1 – m 2 u 2 = (m 1+ m 2) u, откуда u = (m 1 u 1 – m 2 u 2)/(m 1+ m 2) =
= 0,4 (м/с).
Ответ: 2,8 м/с; 0,4 м/с.
Пример 16. Радиус-вектор частицы массы 1 кг зависит от времени по закону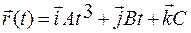 
, где А = 1 м/с3, В = 2 м/с, С = 3 м. Записать закон, по которому со временем изменяется вектор силы, действующей на частицу, и найти модуль скорости частицы через 1 секунду после начала движения.
Дано: ;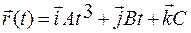
А = 1 м/с3, В = 2 м/с, С = 3 м,;
m = 1 кг.
Найти: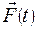 
, v.
Решение. Исходная формула для нахождения зависимости силы от времени – второй закон Ньютона (1.3.40):
= = 
=
= 
.
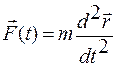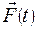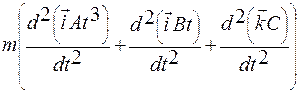Модуль скорости частицы найдем из (1.3.23), используя (1.3.22):
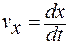= d (At 3)/ dt = 3 At 2 = 3 (м/с),
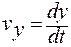= d (Bt)/ dt = B = 2 (м/с),
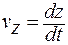= d (C)/ dt = 0.
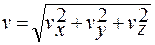= (32 + 22)1/2 = 3,6 (м/с).
Ответ: 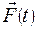= ; v = 3,6 м/с.
Поиск по сайту: