Полная механическая энергия тела. Законы сохранения и изменения энергии

Если частица массы m движется со скоростью v, то ее кинетическая энергия может быть представлена в виде

. (1.3.57)

Кинетическая энергия системы частиц – величина аддитивная и представляет собой сумму кинетических энергий всех частиц системы:

,

где N – число частиц в системе, m_i – масса i -той частицы, v_i – скорость i -той частицы.

* Сила, работа которой не зависит от формы и длины пути (от траектории точки приложения силы), называется консервативной силой. Математически условие консервативности силы выражается в виде:

,

что означает:

* циркуляция консервативной силы по любому замкнутому контуру равна нулю.

Из определения консервативной силы следует:

работу консервативной силы можно представить как убыль некоторой скалярной функции , зависящей только от положения тела (частицы), которая называется потенциальной энергией:

Последняя формула является определением потенциальной энергии:

* Потенциальная энергия определена с точностью до произвольной постоянной.

Так как определена только разность потенциальной энергии, то к выражению для потенциальной энергии можно добавить или вычесть любую постоянную величину. Поэтому в каждом конкретном случае договариваются о начале отсчета потенциальной энергии (в какой именно точке считают U = 0).

Полная механическая энергия частицы – это сумма ее кинетической и потенциальной энергий:

Если на частицу действуют только консервативные силы, то с одной стороны dA = – dU, с другой (из второго закона Ньютона): dA = dK Þ – dU = dK,

d (K + U) = dE=0 Þ

Е = const (1.3.58)

Выражение (1.3.58) – это закон сохранения полной механической энергии, который гласит:

* механическая энергия частицы, подверженной действию только консервативных сил, сохраняется.

Неконсервативные силы – силы, работа которых зависит от длины и формы пути. То есть, работа неконсервативных сил на замкнутом пути не равна нулю, с ними не связана потенциальная энергия.

Примеры: сила трения скольжения, сила вязкого трения.

Работа силы трения скольжения зависит не от перемещения тела, а от длины пути: A _тр = – mNl,и не равна нулю при возвращении тела в исходную точку.

Если на частицу действуют как консервативные, так и неконсервативные силы, то полная механическая энергия этой частицы сохраняться не будет:

dE = d (K + U) = dA _неконс. (1.3.59)

Выражение (1.3.59) является математическим выражением закона изменения полной механической энергии:

* Изменение полной механической энергии частицы равно работе всех действующих на нее неконсервативных сил:

Потенциальная энергия системы частиц складывается из собственной потенциальной энергии U _соб (энергия взаимодействия частиц системы между собой) и внешней потенциальной энергии U _внешн:

U _сист = U _соб + U _внешн,

где

.

Здесь U_ij – потенциальная энергия взаимодействия i -той и j -той частиц системы; коэффициент 1/2 учитывает тот факт, что каждое слагаемое в двойной сумме учитывается дважды.

Если на каждую частицу системы действуют, кроме внутренних, также внешние силы, пусть тоже консервативные, то их работа равна убыли внешней энергии dA = – dU _внешн,

где .

Здесь U_i – потенциальная энергия i -той частицы во внешнем поле. Она зависит от положений всех частиц во внешнем поле и является аддитивной (в отличие от собственной энергии U _соб).

В таком случае, полная механическая энергия системы частиц запишется так:

E = K _сист + U _соб + U _внешн.

* Консервативной называется система, полная механическая энергия которой сохраняется: E _сист = сonst. В такой системе отсутствуют любые неконсервативные силы (и внешние, и внутренние).

Заметим, что консервативность системы и закон сохранения энергии никак не связаны с замкнутостью системы.

Закон изменения полной механической энергии системы:

* Изменение полной механической энергии системы равно суммарной работе всех неконсервативных сил:

dE _сист = dA _неконс.

Кинетическая энергия вращающегося вокруг закрепленной оси твердого тела:

, (1.3.60)

где m_i – масса i -той частицы, R_i – радиус окружности, по которой вращается i -тая частица, w – угловая скорость вращения тела.

Продифференцируем по времени формулу (1.3.60) и получим закон изменения кинетической энергии вращающегося вокруг закрепленной оси твердого тела:

.

то есть,

* скорость изменения кинетической энергии вращательного движения равна мощности результирующего момента сил относительно оси вращения.

Отсюда

dK _вращ = M_zwdt = M_zdj Þ DK º K ₂ – K ₁ = ò M_zd j,

то есть,

* изменение кинетической энергии вращательного движения равно работе момента сил.

Движение твердого тела, при котором центр масс перемещается в фиксированной плоскости, а ось вращения тела, проходящая через его центр масс, остается перпендикулярной к этой плоскости, называется плоским движением. Типичным примером такого движения является качение симметричного тела.

Это движение можно свести к совокупности поступательного движения и вращения вокруг неподвижной (закрепленной) оси.

Кинетическая энергия тела, совершающего плоское движение, запишется в виде

. (1.3.61)

Здесь V_С – скорость движения центра масс тела.

Пример 22. Однородный диск массы 1 кг и радиуса 1 м катится без трения и проскальзывания. Скорость центра масс диска составляет 1 м/с. Найти кинетическую энергию диска.

Дано: m = 1 кг;

R = 1 м;

V_C = 1 м/с.

Найти: К _плоск.

Решение. Данное движение диска является плоским, поэтому для кинетической энергии диска запишем формулу (1.3.61):

.

Найдем момент инерции диска, вращающегося относительно оси, проходящей через его центр масс из (1.3.52):

I_C = (1/2) mR ²,

а угловую скорость вращения диска из (5.17): v = wR.

Имеем:

= =

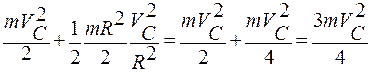= 0,75 (Дж).

Ответ: 0,75 Дж.

Пример 23. Небольшая шайба массы 1 кг, имея начальную скорость 10 м/с, останавливается, пройдя путь, равный 5 м. Найти силу трения, действующую на шайбу.

Дано: m = 1 кг;

V ₀ = 1 м/с;

S = 5 м.

Найти: F _тр.

Решение. В силу того, что во время движения на шайбу действует сила трения, полная механическая энергия шайбы изменяется, причем из (1.3.59) имеем:

dE = d (K + U) = dA _неконс или в интегральной форме, расшифровывая работу силы трения,

DЕ = A _неконс = F _тр× S × cosa = – F _тр× S, (1.3.62)

так как вектор силы трения противонаправлен перемещению шайбы, то есть a = 180°, cos 180° = – 1.

Запишем, чему равно изменение полной механической энергии шайбы, используя (1.3.62):

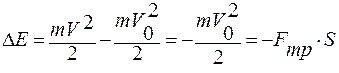, откуда

= 10 (Н).

Ответ: 10 Н.

Пример 24. Резиновая шайба массы 1 кг, двигаясь со скоростью 1 м/с, соскальзывает с горки высотой 1 м и приобретает скорость V у подножия горки. Во время движения над шайбой была совершена работа сил трения А _тр = 1 Дж. Считая, что ускорение свободного падения составляет 10 м/с², найти скорость шайбы V.

Дано: m = 1 кг;

V ₀ = 1 м/с;

А _тр = 1 Дж;

g = 10 м/с².

Найти: V.

Решение. Поскольку во время движения шайбы на нее по условию задачи действует сила трения, полная механическая энергия шайбы изменяется. Запишем закон изменения полной механической энергии в интегральной форме:

DE = Е ₂ – Е ₁ = A _тр.

Изменение полной механической энергии:

, откуда выразим скорость, которую приобретает шайба у подножия горки:

= 4,36 (м/с).

Ответ: 4,36 м/с.

Поиск по сайту: