 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Поляризация электромагнитных волн. Оптически активные среды
В поперечной электромагнитной волне колебания электрического и магнитного полей происходят перпендикулярно направлению движения волны.
Естественным называется свет, в котором колебания вектора напряженности электрического поля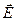 
(или вектора напряженности магнитного поля 
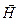) происходят беспорядочно, в любом направлении, перпендикулярно скорости распространения волны:
 |
 |
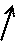
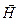
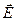
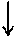
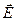
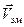
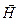
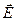
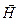
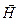
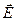
Если колебания светового вектора 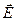как-либо упорядочены, то свет называется поляризованным.
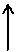
Для плоскополяризованного света колебания светового вектора 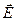происходят все время в одной плоскости:
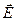
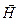
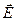
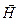
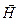
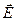
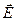
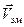
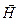
Можно получить световую волну, в которой вектор 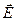будет вращаться вокруг направления скорости волны. Если при вращении вектора 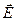вокруг направления скорости волны его конец описывает эллипс, то поляризация называется эллиптической. Если траекторией конца вектора 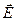является круг, то это свет с круговой поляризацией. Он получится, если сложить две плоскополяризованные во взаимно перпендикулярном направлении световые волны, амплитуды которых одинаковы, а разность фаз равна p /2.
В приведенных выше примерах свет полностью поляризован. Если световой луч складывается из естественного и поляризованного света, то он называется частично поляризованным.
При падении естественного света на границу раздела двух непроводящих сред под углом
aБ = arctg (n2 / n1) (угол Брюстера) (4.3.10)
отраженный луч будет полностью поляризован: колебания вектора 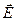в нем происходят только перпендикулярно плоскости падения света.
Если падение света происходит под другим углом a ¹ aБ, то отраженный свет будет частично поляризован. Преломленный луч всегда частично поляризован в плоскости падения света.
На практике для поляризации света используют так называемые поляризаторы – устройства, пропускающие только те электромагнитные волны, в которых вектор 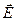колеблется вдоль оси поляризатора. Интенсивность прошедшего света связана с интенсивностью падающего света (если он плоскополяризован) законом Малюса:
Iпрош = Iпад cos 2 a. (4.3.11)
Здесь a – угол между осью поляризатора и направлением поляризации падающего света.
Если на поляризатор падает естественный свет с интенсивностью I0, то после прохождения через поляризатор интенсивность света уменьшается в два раза:
Iпрош = I 0/2. (4.3.12)
При распространении света в среде с показателем преломления n его скорость вычисляется по формуле:
V = c / n, (4.3.13)
где с – скорость света в вакууме (с = 3×108 м/с).
Существуют вещества способные вращать плоскость поляризации света в отсутствии внешних воздействий. Такие вещества называются оптически активными. В качестве примера оптически активных веществ можно привести скипидар, камфору, никотин, киноварь, раствор сахара, биологические макромолекулы и др. При этом, как показали опыты, для данной длины волны света величина угла поворота a плоскости поляризации прямо пропорциональна длине пути луча в оптически активной среде, то есть
a = const×C×l, (4.3.14)
где С – концентрация раствора, l – длина пути луча в оптически активной среде.
Пример 6. Естественный луч света падает на границу раздела жидкость-стекло. Угол между падающим на стекло лучом и отраженным от него лучом составляет 98°. Определить показатель преломления жидкости, если отраженный луч максимально поляризован, а абсолютный показатель преломления стекла равен 1,5. Определить угол преломления, а также скорость распространения луча в стекле и в жидкости.
Дано: 2 a = 98°,
n 2 = 1,5,
Найти: n 1, V 1, V 2, b.
Решение. а) Закон отражения света: угол падения равен углу отражения:
Поскольку по условию задачи отраженный луч полностью поляризован, то угол падения a (и, соответственно, угол отражения) является углом Брюстера, мы можем записать закон Брюстера (4.3.10):
aБ = arctg (n 2/ n 1) = 98°/2 = 49°,
откуда следует, что tgaБ = n 2/ n 1 и n 1 = (n 2/ tgaБ) = 1,3.
б) 180° = aБ + b + g. Когда свет падает под углом Брюстера, угол g равен 90°, поэтому
b = 180° – 90° – aБ = 41°.
Можно найти угол b, используя закон преломления света:
sinaБ / sinb = n 2/ n 1, откуда sinb = (sinaБ× n 1)/ n 2 = 0,654;
b = arcsin (0,654) = 41°.
в) Для расчета скорости распространения света в жидкости и стекле используем формулу (4.3.13):
V = c / n,
для жидкости: V 1 = c / n 1 = 2,3×108 м/с,
для стекла: V 2 = c / n 2 = 2,0×108 м/с.
Ответ: n 1 = 1,3; b = 41°; V 1 = 2,3×108 м/с; V 2 = 2,0×108 м/с.
Пример 7. Естественный свет проходит последовательно через поляризатор и анализатор. Угол между плоскостями поляризатора и анализатора изменили от a = 45° до b = 60°. Во сколько раз при этом уменьшилась интенсивность света, прошедшего через анализатор?
Дано: a = 45°,
b = 60°.
Найти: Ia 1/ Ia 2.
Решение. Запишем закон Малюса (4.3.11) для углов a и b:
Iа 1 = Iп cos 2 a,
Iа 2 = Iп cos 2 b,
где Iа 1 и Iа 2 – интенсивности света, прошедшего первый и второй анализаторы соответственно, Iп – интенсивность света, прошедшего поляризатор.
Разделив первое соотношение на второе почленно, получаем окончательно:
Ia 1/ Ia 2 = cos 2 a / cos 2 b = 2.
Ответ: интенсивность света уменьшится в два раза.
Пример 8. При прохождении через раствор 10%-го раствора сахара толщиной l 1 плоскость поляризации света повернулась на 15°. В другом растворе сахара вдвое большей толщины плоскость поляризации повернулась на 20°. Найти концентрацию второго раствора.
Дано: С 1= 10%,
l 2 = 2 l 1,
a 1 = 15°,
a 2= 20°.
Найти: С 2.
Решение. Запишем исходное выражение (4.3.14) для угла поворота плоскости поляризации света оптически активными средами и применим его для растворов двух рассматриваемых в задаче концентраций:
a 1 = const×C 1 ×l 1 = 15°,
a 2 = const×C 2 ×l 2 = 20°.
Разделим второе выражение на первое почленно и выразим неизвестную концентрацию: 20°/15° = (С 2 × 2 l 1)/(С 1× l 1) = 2 С 2/ С 1,
откуда С 2 = 6,7%.
Ответ: С 2 = 6,7%.
Поиск по сайту: