Пример 6. Критерий Стьюдента

Даны две выборки, взятые из нормально распределенных генеральных совокупностей X и Y, для которых известно:

Объем n _X = 42, выборочное среднее 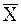= 119, выборочная дисперсия 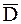_X = 126,9;

Объем n _Y = 35, выборочное среднее = 107, выборочная дисперсия _Y = 136,1.

Проверить гипотезу о равенстве средних при уровне значимости 0,05.

Решение. Выборочные дисперсии близки, поэтому обоснованным является предположение о равенстве генеральных дисперсий. В этом случае можно воспользоваться t -критерием Стьюдента.

Нулевая гипотеза Н₀: генеральные средние двух совокупностей равны;

Альтернативная гипотеза H₁: генеральные средние двух совокупностей различны.

Значение критерия находим по формуле (1.3.10):

Числитель равен

(119 – 107)/[(42×356)/(42 + 35)]^1/2 = 52,4.

Знаменатель равен

[41×127 – 34 × 107]/(42 + 35 – 2)]^1/2 = 11,4.

Значение критерия равно t = 4,58. Критические значения находим по таблицам t -распределения:

Значение критерия принадлежит однопроцентной области. Поэтому нулевая гипотеза отвергается и признается различие между выборками.

Пример 7. Длительность сердечного цикла (в секундах) в кардиограммах у здоровых и больных детей представлена следующими выборками по 60 элементов:

а) здоровые дети – выборка X:

0,91; 0,71; 0,73; 0,82; 0,67; 0,89; 0,90; 1,00; 0,77; 0,78; 0,90; 0,68; 0,52; 0,58; 0,59; 0,66; 0,74; 0,54; 0,72; 0,74; 0,74; 0,79; 0,66; 0,84; 0,85; 0,81; 1,00; 0,77; 0,84; 0,74; 0,65; 0,83; 0,78; 0,93; 0,62; 0,69; 0,57; 0,82; 0,65; 0,74; 0,69; 0,80; 0,78; 0,66; 0,74; 0,68; 0,57; 0,75; 0,69; 0,97; 0,83; 0,78; 0,89; 0,75; 0,68; 0,62; 0,68; 0,85; 0,79; 0,75;

б) больные дети – выборка Y:

0,91; 0,86; 0,74; 1,07; 0,79; 0,89; 0,98; 1,16; 0,77; 0,88; 0,84; 0,68; 0,73; 0,91; 1,12; 0,72; 1,23; 0,64; 0,98; 1,37; 0,77; 0,79; 0,66; 0,85; 0,85; 0,81; 1,00; 1,05; 0,94; 0,86; 0,75; 1,17; 0,78; 0,93; 0,69; 0,99; 1,07; 0,82; 0,95; 0,74; 0,69; 0,80; 0,78; 0,66; 0,74; 1,08; 0,77; 0,75; 0,69; 0,97; 0,83; 0,78; 1,18; 0,75; 0,63; 0,82; 0,89; 0,85; 0,77; 0,75.

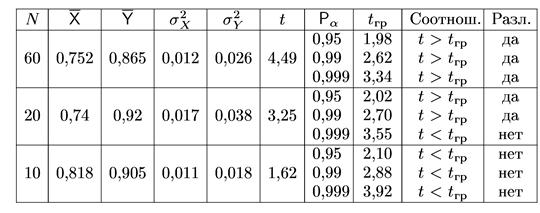
Оценить достоверность различий этой характеристики в представленных выборках. Исследовать влияние объема выборки на результат проверки гипотез. Для этого выполнить процедуру проверки при n равном: а) 10; б) 20; в) 60. Сделать вывод о влиянии объема выборки и доверительной вероятности на оценку достоверности различий.

Решение. Выборочные дисперсии близки, поэтому можно воспользоваться t -критерием Стьюдента.

Нулевая гипотеза H₀: генеральные средние совокупностей равны.

Альтернативная гипотеза H₁: генеральные средние совокупностей различны.

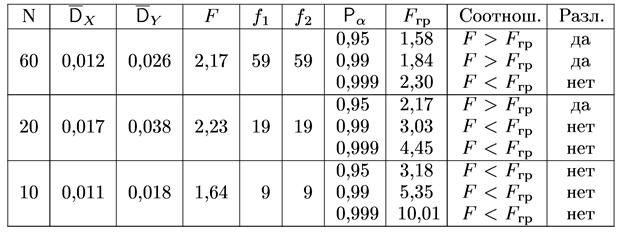
Промежуточные и конечные результаты, полученные при обработке первичной информации, представлены в таблице.

Пример 8. F -критерий Фишера. По исходным данным примера 7 проверить гипотезу о равенстве дисперсий.

Решение. Для проверки воспользуемся F -критерием Фишера.

Нулевая гипотеза H₀: генеральные дисперсии совокупностей равны;

Альтернативная гипотеза H₁: генеральные средние совокупностей различны.

Значение критерия находим по формуле (1.3.11). Промежуточные и конечные результаты, полученные при обработке первичной информации, представлены в таблице.

Пример 9. Критерий Вилкоксона. Получены две независимые выборки, значения элементов которых представлены в порядковой шкале. Требуется проверить гипотезу о принадлежности выборок к одной и той же генеральной совокупности. Решим задачу с помощью непараметрического критерия Вилкоксона.

Проверяемые гипотезы:

Нулевая гипотеза Н₀: выборки принадлежат к одной генеральной совокупности.

Альтернативная гипотеза H₁: выборки принадлежат к различным генеральным совокупностям.

Подготовительная работа выполнена в таблице.

Таблица 3. Объединенная Таблица 4. Данные табл. 3,

выборка по возрастанию разнесенные по выборкам

значений наблюдений с указанием исправленных

рангов

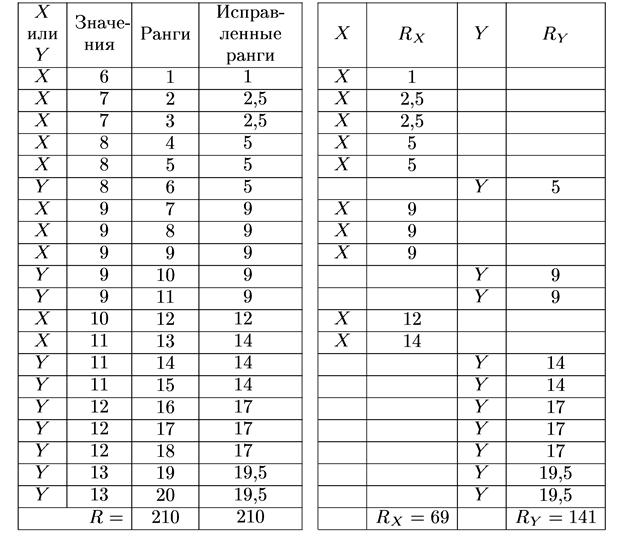R _max = 141, n _max = 10. Граничные значения для 1% и 5% областей равны 19 и 27.

По формуле (1.3.12) вычисляем значение критерия:

U _опыт = 10 ×10 – 141 + 10× 11/2 = 14.

Значение критерия (U = 14) попадает в однопроцентную критическую область. Поэтому нулевая гипотеза отвергается, и различия между выборками являются значимыми.

Поиск по сайту: