 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Принцип суперпозиции для вектора напряженности электрического поля
Взаимодействие между зарядами осуществляется через поле. Всякий электрический заряд q изменяет определенным образом свойства окружающего его пространства – создает электрическое поле. Это поле проявляет себя в том, что помещенный в какую-либо его точку другой, «пробный», заряд испытывает действие силы.
Силовой характеристикой электрического поля является напряженность – это сила, с которой электрическое поле действует на пробный заряд.
Величина напряженности поля неподвижного точечного заряда:
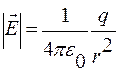. (2.3.1)
Принцип суперпозиции для вектора напряженности электрического поля:
Напряженность системы точечных неподвижных зарядов равна векторной сумме напряженностей полей, которые создавали бы каждый из зарядов в отдельности:
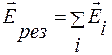. (2.3.2)
Электрическое поле принято изображать с помощью силовых линий – это линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности. Силовые линии электростатического поля не могут начинаться или заканчиваться в вакууме. Они начинаются на положительных и заканчиваются на отрицательных зарядах:
Пример 1. Имеются два точечных заряда q 1=2 нКл, q 2 = 1 нКл, находящиеся на одной прямой на расстоянии r = 50 см друг от друга (по условию задачи заряд q 1расположен слева, заряд q 2 – справа). Найти модуль напряженности электростатического поля в точке О, расположенной между зарядами на расстоянии 10 см от заряда q 2.
Дано: q 1 = 2 нКл = 2×10–9 Кл,
q 2 = 1 нКл = 1×10–9 Кл,
r = 50 см = 0,5 м,
r 2 = 10 см = 0,1 м.
Найти: ½ Е рез½.
Решение. Сделаем рисунок, на котором укажем расположение зарядов и точку О, в которой будем находить модуль результирующей напряженности. Выбираем направление оси x:
2 q1 q 2 1
А О В x
Здесь 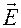1 – напряженность, создаваемая в точке О зарядом q 1, 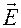2 – напряженность, создаваемая в точке О зарядом q 2. По условию задачи и в соответствии с рисунком, АВ = r = 0,5 м; ОВ = r 2 = 0,1 м; АО = r 1 = АВ – ОВ = r – r 2= 0,5 – 0,1 = 0,4 м.
Запишем исходные формулы – формулу для расчета модуля напряженности поля точечного заряда (2.3.1) и принцип суперпозиции для вектора напряженности поля системы зарядов (2.3.2):
; .
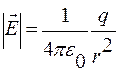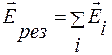Напряженность – это вектор. Чтобы найти модуль напряженности поля системы двух зарядов по формуле (2.3.2), необходимо рассчитать модули напряженностей Е 1 и Е 2, создаваемых зарядами q 1 и q 2 по формуле (1), а потом сложить их с учетом знака. Вектор 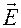2 противоположен выбранному нами направлению оси x, вектор 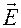1направлен в ту же сторону, что и ось. Имеем:
½ Е рез½ = ½ Е 1 – Е 2½. (2.3.3)
Теперь подставим числовые данные в формулу (2.3.1) и, используя формулу (2.3.3), получим окончательный ответ:
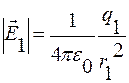= 113 В/м; 
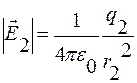= 900 В/м;
Е рез = ½ Е 1 – Е 2 ½= ½113 – 900½ = 787 В/м.
Ответ: Е рез = 787 В/м.
Пример 2. Имеются два точечных заряда q 1=2 нКл, q 2 = –1 нКл, находящиеся на одной прямой на расстоянии r = 50 см друг от друга (по условию задачи заряд q 1расположен слева, заряд q 2 – справа). Найти модуль напряженности электростатического поля в точке О, расположенной между зарядами на расстоянии 10 см от заряда q 2.
Дано: q 1 = 2 нКл = 2×10–9 Кл,
q 2 = – 1 нКл = – 1×10–9 Кл,
r = 50 см = 0,5 м,
r 2 = 10 см = 0,1 м.
Найти: ½ Е рез½.
Решение. Как и в примере 1, сделаем рисунок, на котором укажем расположение зарядов и точку О, в которой будем находить модуль результирующей напряженности.
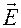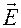q 1 q 2 2 1
А О В x
Здесь 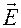1 – напряженность, создаваемая в точке О зарядом q 1, 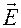2 – напряженность, создаваемая в точке О зарядом q 2. Аналогично предыдущему примеру, АВ = r = 0,5 м; ОВ = r 2 = 0,1 м; АО = r 1 = 0,4 м.
Исходные формулы – формула для расчета модуля напряженности поля точечного заряда (2.3.1) и принцип суперпозиции для вектора напряженности поля системы из двух зарядов (2.3.2).
Как видно из рисунка, оба вектора 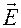2 и 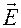1 направлены в ту же сторону, что и ось x, поэтому формулу (2) можно записать как
Е рез = Е 1 + Е 2. (2.3.4)
Теперь подставим числовые данные в формулу (2.3.1) и, используя формулу (2.3.4), получим окончательный ответ:
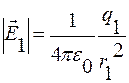= 113 В/м; 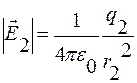= 900 В/м;
Е рез = Е 1 + Е 2 = 1013 В/м.
Ответ: ½ Е рез½ = 1013 В/м.
Поиск по сайту: