Связь вектора напряженности электрического поля и потенциала

Между вектором напряженности электрического поля и потенциалом существует следующая связь:

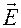= – grad j, (2.3.12)

где – дифференциальный оператор «набла», который является вектором. Действуя на любой скаляр, он превращает его в вектор:

grad j = ,

поэтому

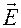= – . (2.3.13)

Как известно, любой вектор можно разложить на проекции по осям координат, то есть

(2.3.14)

Сравнивая формулы (2.3.13) и (2.3.14), получаем:

E_x = – (¶j / ¶x); E_y = – (¶j / ¶y); E_z = – (¶j / ¶z). (15)

Чтобы найти модуль вектора (его абсолютное значение), используют следующую формулу:

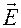| | = E = (E ² _x + E ² _y + E ² _z)^1/2. (2.3.16)

Между силой Кулона , действующей на электрический заряд со стороны электрического поля, и потенциальной энергией W этого заряда в данной точке поля существует связь, аналогичная связи между вектором напряженности и потенциалом:

= – grad W = – , (2.3.17)

причем

F_x = – (¶W/¶x); F_y = – (¶W / ¶y); F_z = – (¶W / ¶z), (2.3.18)

а модуль силы Кулона

| | = F = (F ² _x + F ² _y + F ² _z)^1/2. (2.3.19)

Пример 6. Потенциал электростатического поля зависит от координат по закону j = A . Найти величину напряженности электрического поля в точке Р (x ₀ ,y ₀, z ₀), если А = 3 В, x ₀ = y ₀ = z ₀ = 1 м, b = 1м.

Решение. Запишем исходные формулы (это формулы (2.3.13), (2.3.15), (2.3.16) соответственно):

= – ;

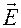E_x = – (¶j/¶x); E_y = – (¶j/¶y); E_z = – (¶j/¶z);

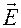| | = E = (E ² _x + E ² _y + E ² _z)^1/2.

Рассчитаем проекции вектора напряженности на оси координат по формуле (2.3.15):

E_x = – (¶j/¶x) = – А (yz/b ³); (2.3.20)

E_y = – (¶j/¶y) = – A (xz/b ³); (2.3.21)

E_z = – (¶j/¶z) = – A (xy/b ³). (2.3.22)

Подставляя в (2.3.20), (2.3.21) и (2.3.22) значения координат x = x ₀, y = y ₀, z = z ₀ получаем:

E_x = – 3 В/м, E_y = – 3 В/м, E_z = – 3 В/м.

Результат подставляем в (2.3.16):

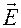| | = E =(E ² _x + E ² _y + E ² _z) ^1/2 = 5,2 В/м.

Ответ: 5,2 В/м.

Пример 7. Потенциальная энергия точечного заряда в электростатическом поле зависит от координат по закону W = A . Найти величину силы Кулона, действующую на этот заряд в точке Р (x ₀ ,y ₀), если А = 2 Дж, x ₀ = y ₀ = z ₀ = 1 м, b = 1м.

Решение. Запишем исходные формулы (это формулы (2.3.17), (2.3.18), (2.3.19) соответственно):

= – grad W = – ,

F_x = – (¶W / ¶x); F_y = – (¶W / ¶y); F_z = – (¶W / ¶z);

| | = F = (F ² _x + F ² _y + F ² _z)^1/2.

Рассчитаем проекции вектора силы Кулона на оси координат по формуле (2.3.18):

F_x = – (¶W / ¶x) = – А (yz ²/ b ⁴); (2.3.23)

F_y = – (¶W / ¶y) = – A (xz ²/ b ⁴); (2.3.24)

F_z = – (¶W / ¶z) = – 2 A (xyz / b ⁴). (2.3.25)

Подставляя в (2.3.23), (2.3.24) и (2.3.25) значения координат x = x ₀, y = y ₀, z = z ₀, получаем:

F_x = – 2 Н, F_y = – 2 В/м, F_z = – 4 В/м.

Результат подставляем в (2.3.19):

| | = F = (F ² _x + F ² _y + F ² _z) ^1/2= 4,9 Н.

Ответ: 4,9 Н.

Поиск по сайту: