Динамика вращательного движения твердого тела

Моментом импульса частицы, движущейся по некоторой траектории и имеющей в данный момент времени радиус вектор и импульс 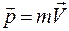, относительно точки (центра) О, называется векторное произведение радиус-вектора и импульса частицы:

. (1.3.43)

Направление определяется правилом правого винта.

Векторное произведение любых векторов определяется следующим образом:

.

Закон изменения момента импульса:

. (1.3.44)

Здесь – момент силы.

* Скорость изменения момента импульса частицы относительно некоторой точки равна моменту силы относительно той же точки.

перпендикулярен векторам и , и образует с ними правую тройку векторов.

ê ê= rFsina, (1.3.45)

l = rsina,

где l – кратчайшее расстояние от точки О до линии действия силы – плечо силы.

Проекция вектора момента силы на некоторую фиксированную (закрепленную) ось, например ось z, называется моментом импульса относительно оси:

L_z = Iw, (1.3.46)

где I – момент инерции частицы,

I = mR ². (1.3.47)

Закон изменения момента импульса относительно оси:

, (1.3.48)

где M_z – проекция момента силы на ось z.

Спроектируем уравнение моментов для системы материальных точек на ось вращения Oz, получим:

или .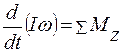

Для абсолютно твердого тела I = const, поэтому

, (1.3.49)

то есть,

* произведение момента инерции на угловое ускорение равно результирующему моменту внешних сил относительно закрепленной оси вращения.

Уравнение (1.3.49) – основное уравнение вращательного движения твердого тела относительно закрепленной оси.

Здесь I играет роль меры инертности (как масса при поступательном движении).

Как следует из основного уравнения,

* Если моменты всех сил относительно оси уравновешены, то есть, S M_z = 0, то момент импульса тела (или системы тел) относительно той же оси сохраняется: L_z = Iw = const. Это частный случай закона сохранения момента импульса.

Момент инерции тела относительно оси равен сумме произведений масс его материальных точек на квадраты их расстояний до оси вращения:

I = S m_iR ² _i.

Поскольку масса твердого тела распределена непрерывно, сумму следует заменить на интеграл. Тело разбивают на бесконечно малые объемы dV с массой dm = rdV.

Таким образом,

I = ò R ² dm = ò R ² rdV, (1.3.50)

где R – расстояние от элемента dV до оси вращения.

Пример 17. Вычислить момент инерции тонкого однородного стержня массы m и длины l относительно оси, проходящей через середину стержня, перпендикулярно ему.

l /2

dm

x

O C dx

ось

Решение. Ось, относительно которой нужно рассчитать момент инерции, проходит через центр масс стержня (точку С), так как по условию задачи он однороден. Выделим элемент массы dm стержня и длины dx. Момент инерции стержня относительно оси, проходящей через его центр масс, найдем из выражения (1.3.50), учитывая, что dV = dx, так как по условию задачи стержень тонкий, а масса единицы объема (в нашем случае масса единицы длины) определяется выражением r = m / l:

.

Пример 18. Рассчитать момент инерции стержня (см. пример 17) относительно оси, проходящей через один из его концов (точку О).

Решение. Согласно (1.3.50),

.

Моменты инерции тел относительно оси, проходящей через центр масс:

Тонкого обруча: I_C = mR ²; (1.3.51)

Диска (цилиндра): I_C = (1/2) mR ²; (1.3.52)

Шара: I_C = (2/5) mR ². (1.3.53)

Если момент инерции I_C относительно оси, проходящей через центр масс, известен, то можно легко вычислить момент инерции относительно любой параллельной ей оси О, проходящей на расстоянии d от центра масс по теореме Штейнера:

* Момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной ей и проходящей через центр масс, и произведения массы тела на квадрат расстояния между осями: