Проверка статистических гипотез

1) t -критерий Стьюдента. t -критерий Стьюдента применяется для оценки различий величин средних двух выборок, которые распределены по нормальному закону с одинаковой дисперсией.

Первичная статистическая информация представляет собой две выборки X = { х_i } и Y = { у_i }, содержащие n _X и n _Y элементов соответственно.

Значение критерия t находят по формуле:

(1.3.10)

где 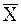, – выборочные средние значения выборок, 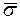_X, 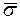_Y – выборочные средние квадратичные отклонения.

Число степеней свободы:

f = n _X + n _Y – 2,

Критическая область для отклонения H₀:

| t | > t _кp.

Критическое значение t _кp находят по таблице t– распределения.

2) F -критерий Фишера. F -критерий Фишера используют для проверки гипотезы о равенстве генеральных дисперсий двух нормальных выборок.

Первичная статистическая информация представляет собой

две выборки X = { х_i } и Y = { у_i }, содержащие n _X и n _Y элементов соответственно.

Значение критерия F находят по формуле:

F = 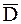_Y/ 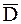_X, (1.3.11)

где 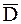_Y – большая выборочная дисперсия, a 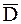_X – меньшая.

Число степеней свободы для каждой выборки:

f ₁ = (n _Y – 1), f ₂ = (n _X – 1),

где f ₁ и f ₂ число степеней свободы числителя и знаменателя, соответственно.

Критическая область для отклонения H₀:

F > F _кp.

Критическое значение F _кp находят по таблице F -распределения.

3) Критерий Вилкоксона. Критерий Вилкоксона применяется для проверки гипотезы о принадлежности сравниваемых независимых выборок, к одной и той же генеральной совокупности, когда данные представлены в порядковой или ранговой шкале. Первичная статистическая информация представляет собой две выборки содержащие n _X и n _Y элементов, значения которых представлены в порядковой шкале.

Подготовительная работа. Составляется объединенная выборка, элементы которой упорядочиваются. В результате получается таблица, в первой строке которой указана принадлежность элемента, во второй строке указаны значения элементов, а в третьей строке стоят порядковые номера элементов упорядоченного ряда от 1 до n _X + n _Y.

Если в таблице встречаются одинаковые значения, то им следует присвоить одинаковые ранги, равные среднеарифметическому значению рангов одинаковых элементов. После этого находят суммы рангов для каждой выборки R _X и R _Y.

Значение критерия U находят по формуле:

U = n _X × n _Y – R _m + n _m × (n _m + 1)/2, (1.3.12)

где n _m – число членов в выборке с максимальным значением суммы рангов.

Критическая область для отклонения Н₀:

U < U _кp.

Критическое значение U _кp находят по таблице F -распределения.

Поиск по сайту: