Кинематика поступательного движения материальной точки

Механика представляет собой учение о простейшей форме движения материи, которое состоит в перемещении тел или их частей друг относительно друга. Кинематика изучает движение тел вне зависимости от тех причин, которые обусловливают это движение.

Иногда при рассмотрении движения тел можно пренебречь их размерами. Тело, размерами которого в условиях данной задачи можно пренебречь, называется материальной точкой.

Поступательное движение – это такое движение, при котором любая прямая, связанная с движущимся телом, остается параллельной самой себе.

Материальная точка при своем движении описывает некоторую линию – траекторию.

Путь (S) – это длина траектории.

Если тело движется из точки 1 в точку 2, то вектор, проведенный из точки 1 в точку 2, называется перемещением ().

Векторный способ описания движения.

Положение материальной точки в пространстве можно задать с помощью ее радиус-вектора . При движении точки конец радиус-вектора описывает ее траекторию, а сам изменяется и по величине, и по направлению.

= (t) – кинематический закон движения точки (уравнение траектории).

Пусть тело движется из точки с радиус-вектором ₁ в точку с радиус-вектором ₂. За время Dt оно совершит перемещение D = ₂ – ₁ и пройдет путь, равный DS (см. рис.).

y

DS

D

_{1 2}

O x

При бесконечно малом перемещении бесконечно малый промежуток времени можно обозначить как dt, тогда ½ d ½= dS.

Скорость – это предел, к которому стремится отношение при неограниченном убывании Dt:

= . (1.3.13)

Модуль скорости: v = ½ ½= . (1.3.14)

Вектор скорости направлен по касательной к траектории.

Средняя скорость:

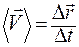или . (1.3.15)

Движение, при котором скорость, изменяясь как угодно по направлению, остается постоянной по величине, называется равномерным. При таком движении скорость равна пути S, деленному на время t, за которое он пройден:

v = S / t. (1.3.16)

Если при движении тела изменяется величина скорости, то такое движение называют ускоренным.

Ускорение определяется как предел, к которому стремится отношение приращения вектора скорости D к промежутку времени Dt, за который оно возникает, при условии, что Dt ®0:

. (1.3.17)

Прямолинейное движение с постоянным ускорением называется равнопеременным.

Кинематика движения материальной точки с постоянным ускорением:

; (1.3.18)

. (1.3.19)

Прямая задача кинематики позволяет найти при заданном уравнении траектории скорость и ускорение материальной точки:

Þ .

Обратная задача кинематики позволяет найти при заданных ускорении или скорости уравнение траектории материальной точки:

; . (1.3.20)

Координатный способ описания движения.

Если с телом отсчета жестко связать какую-нибудь координатную систему (например, декартову), то положение частицы (материальной точки) в любой момент времени определяется тремя ее координатами x (t), y (t), z (t):

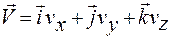; ; . (1.3.21)

Здесь . (1.3.22)

Формулы для определения пройденного пути, модулей скорости частицы и ее ускорения:

; (1.3.23)

Обратная задача кинематики:

; ;

Кинематика движения материальной точки с постоянным ускорением:

. (1.3.24)

.

(1.3.25)

В случае движения материальной точки по произвольной плоской кривой вектор полного ускорения будет равен

, (1.3.26)

где

, .

Вектор _t – тангенциальное ускорение. Он характеризует изменение скорости по величине. Если скорость по величине не изменяется, тангенциальное ускорение равно нулю и = _n.

Вектор _n – нормальное (центростремительное) ускорение. Он характеризует изменение скорости частицы по направлению. Если направление скорости не изменяется, движение происходит по прямолинейно траектории. Кривизна прямой равна нулю (R = = ¥).

Модуль полного ускорения:

, (1.3.27)

где

.

Между линейными и угловыми величинами существует следующая связь:

а _t = eR, (1.3.28)

v = wR, (1.3.29)

a _n = v ²/ R. (1.3.30)

Здесь w – угловая скорость тела, e – угловое ускорение.

Пример 10. Радиус-вектор частицы изменяется со временем по закону , где А = 1 м/с², В = 2 м/с, С = 1 м. Частица движется из начала координат. Найти через 2 секунды после начала движения: 1) путь, пройденный частицей; 2) величину скорости частицы; 3) величину ускорения частицы.

Дано: ;

А = 1 м/с², В = 2 м/с, С = 1 м;

t = 2 c.

Найти: S, v, a.

Решение. Путь, пройденный частицей за 2 секунды после начала движения найдем из (1.3.23) с учетом (1.3.21):

, где x = At ² = 1×(2²) = 4 (м), y = Bt = 2×2 = 4 (м), z = C = 1 (м).

Подставим полученные значения координат частицы в (1.3.23) и рассчитаем пройденный частицей путь:

= 5,7 (м).

Величину скорости и ускорения частицы через указанный в условии задачи промежуток времени также найдем, используя формулу (1.3.23) с учетом (1.3.22):

, где

,

то есть

v_x = d (At ²)/ dt = 2 At = 4 (м/с); v_y = d (Bt)/ dt = B = 2 (м/с);

v_z = d (C)/ dt = 0.

v = (4² + 2² + 0²)^1/2 = 4,5 (м/с).

a_x = d (2 At)/ dt = 2 A = 2 (м/с²); a_y = d (B)/ dt = 0; a_z = 0,

a = (2² + 0² + 0²)^1/2 = 2 (м/с²).

Ответ: 5,7 м; 4,5 м/с; 2 м/с².

Пример 11. Частица начала движение из начала координат по плоской криволинейной траектории радиуса 1 м. Радиус-вектор частицы зависит от времени по закону 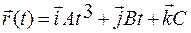, где А = 1 м/с³, В = 2 м/с, С = 3 м. Найти модуль нормального ускорения частицы через 1 секунду после начала движения.

Дано: ;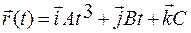

А = 1 м/с³, В = 2 м/с, С = 3 м;

t = 1 с.

Найти: a _n.

Решение. Модуль нормального ускорения найдем с помощью формулы (1.3.30), учитывая (1.3.23) и (1.3.22):

a _n = v ²/ R,

где

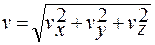, а проекции скоростей на оси координат

.

Подставим в вышеприведенные формулы числовые данные, получим:

v_x = d (At ³)/ dt = 3 At ² = 3 (м/с); v_y = d (Bt)/ dt = B = 2 (м/с);

v_z = d (C)/ dt= 0.

v = (3² + 2² + 0²)^1/2 = 3,6 (м/с); a _n = v ²/ R = 3,6²/1 = (13 м/с²).

Ответ: 13 м/с².

1.3.6. Кинематика вращательного движения вокруг неподвижной оси

Абсолютно твердое тело (АТТ) – это система частиц, расстояния между которыми в процессе движения тела неизменны.

Всякое движение твердого тела можно разложить на два основных движения – поступательное и вращательное.

При вращательном движении все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Ось вращения может находиться вне тела.

Радиус-вектор каждой точки (вектор, проведенный из центра соответствующей окружности в данную точку) поворачиваются за время Dt на один и тот же угол Dj – угол поворота твердого тела.

Поворот тела на некоторый угол (бесконечно малый) dj задают в виде отрезка, длина которого равна dj, а направление совпадает с осью, вокруг которой совершен поворот.

Векторы типа , направление которых связывается с направлением вращения (или обхода), называют аксиальными векторами.

Векторная величина

(1.3.31)

называется угловой скоростью АТТ. Вектор направлен (как и ) вдоль оси, вокруг которой вращается тело в сторону, определяемую правилом правого винта, и представляет собой аксиальный вектор.

При равномерном вращении

w = j / t. (1.3.32)

При одном полном обороте на время t = T тело поворачивается на угол j = 2 p:

w = 2 p / T Þ T = w /2 p, (1.3.33)

где Т – период вращения.

Число оборотов в единицу времени называется частотой вращения:

n = 1/ Т = w /2 p. (1.3.34)

При неравномерном вращении говорят, что тело вращается с ускорением (угловым)

. (1.3.35)

При увеличении угловой скорости со временем вектор угловой скорости и вектор углового ускорения сонаправлены (ускоренное движение). В случае замедленного движения эти векторы противонаправлены.

Обратная задача кинематики вращательного движения:

. (1.3.36)

Для равноускоренного (равнозамедленного) вращения:

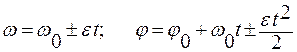. (1.3.37)

Пример 12. Частица из состояния покоя начала ускоренное вращение по окружности радиуса 1 м, угол поворота зависит от времени по закону j (t) = Аt ³. Найти через 1 секунду после начала движения: 1) отношение тангенциального и нормального ускорений; 2) величину полного ускорения частицы. А = 1 рад/с³.

Дано: j (t) = Аt ³,

R = 1 м,

t = 1 с.

Найти: 1) а _t/ а _n; 2) a.

Решение. Тангенциальное и нормальное ускорения частицы найдем с помощью формул (1.3.28) и (1.3.30) с учетом (1.3.29), (1.3.31) и (1.3.35):

а _t = eR, e = dw / dt, w = dj / dt = d (Аt ³) dt = 3 At ² = 3(рад/с). e = d (3 At ²) dt = 6 At = 6 (рад/с²), откуда а _t = 6 (м/с²).

Нормальное ускорение: a _n = v ²/ R, связь между линейной и угловой скоростями: v = wR = 3 (м/с), поэтому a _n= 3²/1 = 9 (м/с²).

Отношение тангенциального и нормального ускорений:

а _t/ a _n = 6/9 = 0,67.

Полное ускорение частицы найдем из (1.3.27):

= (9² + 6²)^1/2 = 10,8 (м/с²).

Ответ: 0,67; 10,8 м/с².

Пример 13. Диск радиуса 1 м начал вращаться вокруг своей оси так, что угол его поворота зависит от времени по закону

j (t) = Аt ³ – В t ². Через сколько секунд диск остановится, если

А = 1 рад/с³, В = 1 рад/с²?

Дано: j (t) = Аt ³ – В t ²;

R = 1 м;

А = 1 рад/с³, В = 1 рад/с².

Найти: t.

Решение. Время остановки диска находим из условия, что его конечная угловая скорость равна нулю: w = 0.

Вращение диска по условию задачи не является равнопеременным, поэтому для нахождения зависимости угловой скорости от времени используем формулу (1.3.31):

, откуда w = dj / dt = d [ Аt ³ – Вt ²]/ dt = 3 At ² –

– 2 Bt.

Теперь используем условие равенства нулю угловой скорости, приравняв к нулю полученное выражение, и найдем время остановки диска:

3 At ² – 2 Bt = 0 Þ t (3 At – 2 B) = 0.

Имеем два корня уравнения:

t ₁ = 0 и t ₂ = 2 B /3 A = 0,67 (с).

Ответ: диск остановится через 0,67 секунды.

Поиск по сайту: