Приведенная теплота.Энтропия

Обратимый цикл Карно. Для обратимого цикла коэффициент полезного действия можно вычислить по любой из полученных ранее формул

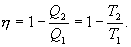Отсюда
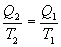или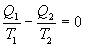

- количество тепла, подводимое к системе в процессе перехода из состояния 1 в состояние 2. - отведенное тепло в течение изотермического процесса 3-4. Или для случая отвода тепла можно сказать, что к системе подведено 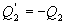тепла

Из рассмотренного цикла Карно видно, что равны между собой отношения теплоты к температурам, при которых они были получены или отданы в изотермическом процессе:

.

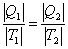Отношение теплоты Q в изотермическом процессе к температуре, при которой происходила передача теплоты, называется приведенной теплотой :

.

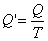Для подсчета приведенной теплоты в произвольном процессе необходимо разбить этот процесс на бесконечно малые участки, где Т можно считать константой. Приведен теплота на таком участке будет равна
Суммируя приведенную теплоту на всех участках процесса, получим:

.

Тогда в обратимом цикле Карно имеем:

Этот результат справедлив для любого обратимого процесса.
Таким образом, для процесса, происходящего по замкнутому циклу

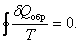
(6.1.2)

Из равенства нулю интеграла, взятого по замкнутому контуру, следует, что подынтегральное выр-ние есть полный дифференциал некот функции, кот опред-ся только состоянием системы и не зависит от пути, каким система пришла в это состояние. Это позволяет ввести новую функцию состояния S:

.

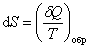(6.1.3)

Функция состояния, полный дифференциал которой равен , называется энтропией (от греч. entropia – поворот, превращение) – мера способности теплоты превращаться в другие виды энергии.
Энтропия S – это отношение полученной или отданной теплоты к температуре, при которой происходил этот процесс.
Понятие энтропии впервые введено Р. Клаузиусом в 1854 г.

Для обратимых процессов изменение энтропии, как следует из (6.1.2),

.

(6.1.4)

Это выражение называется равенство Клаузиуса.

Поиск по сайту: