Описание систем, состоящих из большого числа частиц

Обобщенные координаты – любые параметры, определяющие конфигурацию системы в данный момент.

В простейшем случае – декартовы координаты x, y, z. f – число степеней свободы частицы (для материальной точки f = 3) 1 частица:

1-й индекс – номер частицы;

2-й индекс – степень свободы частицы.

Система из N частиц:

Обобщенные координаты системы из N частиц: 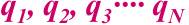Обобщенная координата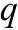

Обобщенная скорость

Обобщенный импульс

Обобщенные импульсы системы из N частиц:

Состояние системы полностью определено, если известно 2fN значений независимых обобщенных координат и импульсов: Совокупность этих 2fN величин

определяет состояние системы или ее фазу Наиболее общая задача статистич физики – проблема расчета распределения энергии в

заданной системе.

Энергия является функциейкоординат (потенциальная)и скоростей или импульсов (кинетическая).

Например, кинетическая энергия частицы связана с обобщенной скоростью следующим образом

Энергия системы. Гамильтониан. Е – полная энергия системы

Гамильтониан системы

Канонические уравнения Гамильтона

9. Фазовое пространство. Изображение состояния системы в фазовом пространстве. Для описания состояния системы и ее эволюции во времени вводится условное фазовое пространство.

Координатами данного пространства являются параметры состояния системы:

Изображение состояния системы на графике

Система: одна точка движется по прямой

Фазовое пространство – многомерное пространство обобщенных координат и

импульсов системы.

Фазовое точка –точка в фазовом пространстве, изображающая состояние системы.

Фазовая траектория – совокупность фазовых точек, показывающая изменение состояния системы.

Фазовое пространство -многомерное (2fN) простран-

ство обобщенных координат и импульсов системы.

Изменение состояния системы происходит в соответствие с уравнениями

Гамильтона (Ньютона) и начальными условиями.

Так как уравнения Гамильтона однозначно определяют поведение системы, то фазовые траектории статистического ансамбля

не пересекаются в фазовом пространстве. Через каждую точку фазового пространства проходит только одна траектория.

μ (мю) - пространство

Фазовое пространство, описывающее одну частицу. Для молекулы идеального газа это 6-мерное пространство

(f = 3)

3 координаты q: x, y, z

3 координаты p: 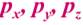Γ (гамма) - пространство

Вводится для описания системы из N частиц.

Пространство 2fN измерений.

Для 1 моля газа (≈ 20 л) N ≈ 10 23

μ – пространство – частный случай

Г- пространства для N = 1

Термины ввел П.Эренфест (голл.)

Описание статистического ансамбля систем в фазовом пространстве

Статистический ансамбль – совокупность большого числа систем (одно и то же макросостояние и разные микросостояния).

В какой-нибудь произвольный момент времени состояние ансамбля в фазовом Г-пространстве изобразится совокупностью отдельных фазовых точек.

Со временем системы ансамбля меняются (точки в фазовом пространстве движутся по фазовым траекториям).

Со временем системы ансамбля меняются (точки в фазовом пространстве движутся по фазовым траекториям).

Аналогия – движение взвешенных частиц в воде.

Каждая частица движется так, будто других не существует.

Т.е. точки в фазовом пространстве представляют собой объемное «многомерное» облако, причем в различных местах Г-пространства плотность фазовых точек различна

Фазовый объем Число систем (фазовых точек) dN, попадающее в выделенный объем dГ фазового пространства зависит от:

1) величины объема dГ 2) области Г-пространства 3) времени

плотность распределения систем ансамбля в фазовом пространстве 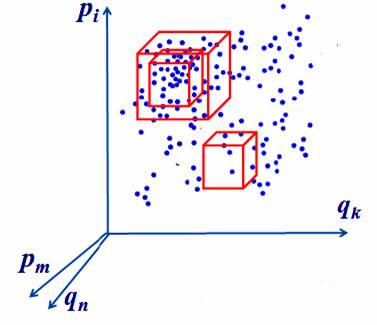Тогда

Вероятность попадания одной системы в фазовый объем dГ

Плотность вероятности

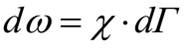
Номировка вероятности Статистическое равновесие При статистическом равновесии плотность распределения ρ систем ансамбля в фазовом пространстве зависит только от координат фазового пространства Так как параметры q и p определяют энергию Е системы, то Одна из основных задач статистической физики – находить распределение систем по энергиям.

Поиск по сайту: