 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Закон возрастания энтропии
1) Энтропия и ее термодинамический смысл: 
 Энтропия – это такая функция состояния системы, бесконечно малое изменение которой в обратимом процессе равно отношению бесконечно малого количества теплоты, введенного в этом процессе, к температуре, при которой оно вводилось.
Энтропия – это такая функция состояния системы, бесконечно малое изменение которой в обратимом процессе равно отношению бесконечно малого количества теплоты, введенного в этом процессе, к температуре, при которой оно вводилось.
В конечном обратимом процессе изменения энтропии может быть подсчитано по формуле:

где интеграл берется от начального состояния 1 системы до конечного состояния 2.
В любом обратимом процессе изменения энтропии равно 0
 (1)
(1)
В термодинамике доказывается, что S системы совершающей необратимой цикл возрастает Δ S > 0 (2)
Выражения (1) и (2) относятся только к замкнутым системам, если же система обменивается теплотой с внешней средой, то её S может вести себя любым образом.
Соотношения (1) и(2) можно представить в виде неравенства Клаузиуса
ΔS ≥ 0
т.е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов) либо оставаться постоянной (в случае обратимых процессов).
Если система совершает равновесный переход из состояния 1 в состояния 2, то изменения энтропии

где dU и δA записывается для конкретного процесса. По этой формуле Δ S определяется с точностью до аддитивной постоянной. Физический смысл имеет не сама энтропия, а разность энтропий. Найдем изменение энтропии в процессах идеального газа.



т.е. изменения энтропии S Δ S 1→2 идеального газа при переходе его из состояния 1 в состояния 2 не зависит от вида процесса.
Т.к. для адиабатического процесса δ Q = 0, то Δ S = 0 => S = const, то есть адиабатический обратимый процесс протекает при постоянной энтропии. Поэтому его называют изоэнтропийным.
При изотермическом процессе (T = const; T 1 = T 2:  )
)

При изохорном процессе (V = const; V 1 = V 2;  )
)

Энтропия обладает свойством аддитивности: энтропия системы равна сумме энтропий тел входящих в систему. S = S1 + S2 + S3 +... Качественным отличием теплового движения молекул от других форм движения является его хаотичность, беспорядочность. Поэтому для характеристики теплового движения необходимо ввести количественную меру степени молекулярного беспорядка. Если рассмотреть какое-либо данное макроскопическое состояния тела с определенными средними значениями параметров, то оно есть нечто иное, как непрерывная смена близких микросостояний, отличающихся друг от друга распределением молекул в разных частях объема и распределяемой энергией между молекулами. Число этих непрерывно сменяющих друг друга микросостояний характеризует степень беспорядочности макроскопического состояния всей системы, w называется термодинамической вероятностью данного микросостояния. Термодинамическая вероятность w состояния системы — это число способов, которыми может быть реализовано данное состояния макроскопической системы, или число микросостояний, осуществляющих данное микросостоян (w ≥ 1, а математическая вероятность ≤ 1).
За меру неожиданности события условились принимать логарифм его вероятности, взятый со знаком минус: неожиданн состояния равна = - 
Согласно Больцману, энтропия S системы и термодинамическая вероятность связаны между собой следующим образом:
S= 
где  - постоянная Больцмана (
- постоянная Больцмана ( ). Таким образом, энтропия определяется логарифмом числа состояния, с помощью которых может быть реализовано данное микросостояние. Энтропия может рассматриваться как мера вероятности состояния т/д системы. Формула Больцмана позволяет дать энтропии следующее статистическое толкования. Энтропия является мерой неупорядоченности системы. В самом деле, чем больше число микросостояний реализующих данное микросостояние, тем больше энтропия. В состоянии равновесия системы - наиболее вероятного состояния системы – число микросостояний максимально, при этом максимальна и энтропия.
). Таким образом, энтропия определяется логарифмом числа состояния, с помощью которых может быть реализовано данное микросостояние. Энтропия может рассматриваться как мера вероятности состояния т/д системы. Формула Больцмана позволяет дать энтропии следующее статистическое толкования. Энтропия является мерой неупорядоченности системы. В самом деле, чем больше число микросостояний реализующих данное микросостояние, тем больше энтропия. В состоянии равновесия системы - наиболее вероятного состояния системы – число микросостояний максимально, при этом максимальна и энтропия.
Т.к. реальные процессы необратимы, то можно утверждать, что все процессы в замкнутой сис-ме ведут к увеличению ее энтропии - принцип возрастания энтропии. При статистич толковании энтропии это означает, что процессы в замкнутой системе идут в направлении увеличения числа микросос, иными словами, от менее вероятных состояний к более вероятным, до тех пор, пока вероятность состояния не станет максим.
Закон возрас энтропии и составляет основ содержа второго начала термодинамики, которое в наиболее общем виде формулируется так:
В замкнутой системе все необрат процессы протекают в направлении возраст энтропии; в частном случае, когда процессы, протекающие в замкнутой системе, обратимы, энтропия системы остается постоянной.
Более кратко второе начало термодинамики может быть сформулировано следующим образом:
В замкнутой системе энтропия никогда не убывает, она либо возрастает, либо остается неизменной, т. е. в замкнутой системе всегда
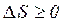 (9) (9)
|
Где знак равенства относиться к обратимым процессам, а знак неравенства ― к необратимым





Термич и калорическое урав состояния. Связь этих уравнений.





Поиск по сайту: