Микро- и макросостояния. Вероятности состояний

Пусть имеется система, состоящая из большого числа частиц.

Макроописание (макросостояние) Известно небольшое число макропараметров (p, V, T) Микроописание (микросостояние) Известны микропараметры каждой частицы (m0, ʋ, x, y, z)

Проблема – определить вероятности микросостояний и макросостояния системы. Определить связь между этими вероятностями. Рассмотрим систему, состоящую из N частиц.1 частица – f степеней свободы.

Число параметров, описывающих положение и движение 1 частицы (координаты, импульс) - 2f

Число параметров, описывающих положение и движение системы из N частиц (координаты, импульсы) - 2fN Метод ячеек Объем ячейки

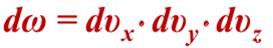Всего ячеек

Вероятность нахождения одной молекулы в первой ячейке Вероятность нахождения 2-х молекул в первой ячейке ... Вероятность нахождения молекул в первой ячейке

Вероятность данного распределения молекул по ячейкам скоростей (вероятность микросостояния)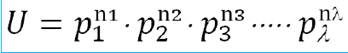

Каждому микросостоянию соответствует одно макросостояние

Каждому макросостояниюсоответствуют много микросостояний

Разные микросостояния, но одно макросостояние Людвиг Больцман-Все микросостояния, характеризующиеся данным распределением молекул по ячейкам равновероятны

Для нахождения вероятности макросостояния нужно сложить вероятности всех микросостояний, с помощью которых оно реализовано.А т.к. эти микросостояния равновероятны, то можно умножить вероятность одного микросостояния на число перестановок, которыми реализуется данное макросостояние. Вероятность макросостояния молекул - перестановок

- общее число перестановок

Перестановки внутри ячейки не меняют микросостояния.

- общее число перестановок - число перестановок в первой ячейке - число перестановок во второй ячейке

Вероятность макросостояния

Объемы ячеек одинаковые, т.е.

- объем одной ячейки - количество ячеек Общий объем ячеек Вероятность попадания 1 молекулы в ячейку Вероятность микросостояния

Вероятность макросостояния

Поиск по сайту: