Флуктуации. Описание и проявления флуктуаций в физических процессах

Флуктуация (от лат. fluctuatio — колебание) – случайное отклонение физической величины от среднего значения. Термодинамическая вероятность системы из N частиц, при приближении к состоянию термодинамического равновесия возрастает. При достижении состояния равновесия термодинамическая вероятность системы достигает максимума. Макроскопические параметры системы (давление газа,его плотность в разных частях системы и др.) в состоянии термодинамического равновесия перестают меняться и остаются практически постоянными. Однако, за счет хаотического движения молекул происходят незначительные отклонения физических параметров от средних значений – флуктуации.

Изменение числа молекул в левой половине ящика после поднятия перегородки

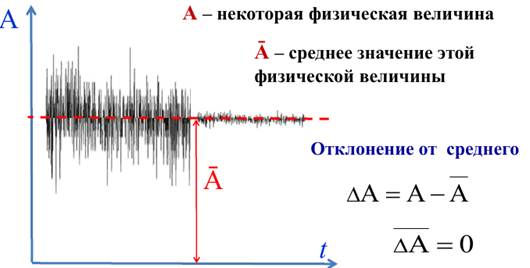
Среднее квадратичное отклонение от среднего (дисперсия)

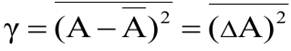
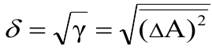Флуктуация (стандартное отклонение) 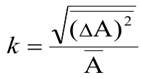Относительная флуктуация

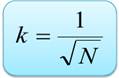Зависимость относительной флуктуации от числа

частиц системы Относительная флуктуация становится значительной и заметной при малом числе частиц в системе

Проявления флуктуаций

1.Броуновское движение – беспорядочное движение малых частиц, взвешенных в жидкости или газе, происходящее под действием ударов молекул окружающей среды. Причины броуновского движения тепловое движение молекул среды и отсутствие точной компенсации ударов, испытываемых частицей со стороны окружающих еѐ молекул, т. е. броуновское движение обусловлено флуктуациями давления.

Закон Эйнштейна 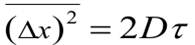Средний квадрат проекции смещения броуновской частицы на какую-либо ось координат (в отсутствие других внешних сил) пропорционален времени τ

2. Флуктуации плотности воздуха Формула Рэлея

Рассеяние света на флуктуациях плотности воздуха Голубой цвет неба

3. Предел чувствительности измерительных приборов Дробовой шум — беспорядочные флуктуации напряжений и токов относительно их среднего значения в цепях радиоэлектронных устройств, обусловленные дискретностью носителей электрического заряда — электронов.

Грубо говоря, прибытие каждого электрона сопровождается всплеском тока в цепи.Дробовой шум проявляется, например, в виде акус-

тического шума в динамике радиоприѐмника, в виде «снега» на экране телевизора, колебаний показания сверхчувствительных приборов.

7. Метод Гиббса. Статистический ансамбль. Эргодическая гипотеза. Изучение различных статистических систем, т.е. систем, состоящих из огромного числа частиц. Разработка единого, принципиально простого метода, составляющего основу современной статистической

физики. Джозайя Уиллард Гиббс (США) в1902 г.написал книгу «Основные принципы статистической механики» Цель статистического исследования – описание и объяснение макроскопических свойств системы, состоящей из огромного числа частиц, на основе анализа микропараметров. Макроскопические величины получаются как интегральные и усредненные микроскопические параметры. Наиболее общая задача статистической физики – проблема расчета распределения энергии в заданной системе.

Основа метода Гиббса – замена эволюции данной системы во времени на изучение совокупности многих аналогичных систем.

Астрономия: замена изучения эволюции звезд анализом состояния многих звезд, существующих в данный момент.

Биология: изучение развития дерева – анализ состояния многих деревьев, находящихся в разных фазах развития.

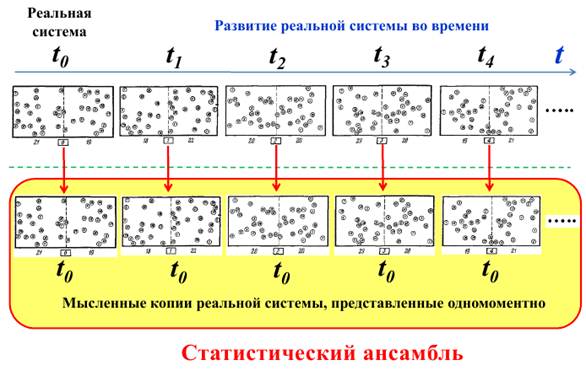
Взамен одной системы, развивающейся во времени, рассматриваются множество систем, существующих одномоментно. Такое собрание аналогичных между собой систем называется статистическим ансамблем

Статистический ансамбль - совокупность очень большого числа одинаковых физических систем многих частиц («копий» данной системы), находящихся в одинаковых макроскопических состояниях; при этом микроскопические состояния системы могут различаться, но совокупность их обязательно должна отвечать заданным значениям макроскопических параметров, определяющих еѐ макроскопическое состояние.

Физическим основанием введения понятия статистического ансамбля является эргодическая гипотеза: Средние по времени значения физических величин, характеризующих систему, равны их средним статистическим значениям этих величин по ансамблю. Эргодическая (от греч. йrgon — работа и hodуs — путь)

Каждая система ансамбля, развиваясь во времени от t = t0 до t → ∞, пройдет через состояния, характеризующие другие системы ансамбля в момент времени t = t0

Строго эргодических систем не существует.

Физики впервые смогли экспериментально подтвердить положения эргодической теории - теории, объясняющей свойства динамически систем. Исследование сразу двух коллективов ученых (Германия) появилось в журнале Angewandte Chemie. Коротко о нем пишет портал Physics World. Динамическими системами называют системы, которые

эволюционируют с течением времени. В динамических системах определенного типа - эргодических - отдельные молекулы движутся так же "случайно", как и вся система в целом. Иными словами, последовательные и усредненные измерения состояний отдельной частицы дают тот же результат, что и измерения состояния всей системы в целом В итоге ученые показали, что измерения, выполненные для отдельных

молекул и для системы в целом, дают идентичные результаты.

Система в термодинамическом равновесии, т.е. макроскопическое состояние неизменно

Примеры статистических ансамблей

Энергетически изолированная система при заданном значении полной энергии – микроканонический ансамбль Гиббса

Система в контакте с термостатом заданной температуры - канонический ансамбль Гиббса Система в контакте с термостатом и резервуаром частиц –большой канонический ансамбль Гиббса

Поиск по сайту: