Н-теорема Больцмана

Применение механических (динамических) закономерностей для анализа процессов в системах, даже состоящих из огромного числа частиц, должны приводить к обратимости процессов в системах любой степени сложности. Ведь огромное число столкновений молекул в газе формально может быть сведено к рассмотрению единичных процессов столкновения молекул, которые являются обратимыми, как является практически обратимым столкновение двух биллиардных шаров.

Тем не менее на практике очень большое число хаотично движущихся частиц (макроскопическое тело) обуславливают определенную направленность процесса.

Т.е. процесс в реальности является необратимым, а энтропия системы растет. Людвиг Больцман попытался обосновать рост энтропии в сложных системах только законами механики, т.е. динамическими закономерностями. При этом Больцман рассматривал динамику ударов молекул газа в некотором объеме.

Больцман использовал функцию распределения молекул газа по скоростям и координатам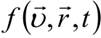

Далее при анализе движения молекул Больцман ввел в

рассмотрение так называемую Н-функцию:

Больцман показал, что Н-функция связана с энтропией газа S следующим образом: причем Н-функция изолированной системы самопроизвольно монотонно убывает со временем. Н – теорема Больцмана Следовательно и энтропия изолированной системы

должна самопроизвольно монотонно возрастать со временем, что и является одной из формулировок Второго начала термодинамики. Таким образом, кажется, что Н-теорема Больцмана на основе только динамических закономерностей обосновывает рост энтропии в сложных системах. Возражения против Н-теоремы Больцмана И. Лошмидт: «Каждому движению молекул газа с убыванием Н-функции соответствуют движения с ее возрастанием»Ответ Больцмана на возражения «Н-теорема не сводится только к динамическим закономерностям, а имеет статистическое толкование. В ней используется предположение о «молекулярном хаосе», которое имеет вероятностный статистический характер».

Поиск по сайту: