 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Соотношения Максвелла
Метод термодинамических потенциалов помогает преобразовывать выражения, в которые входят основные термодинамические переменные и тем самым выражать такие «труднонаблюдаемые» величины, как количество теплоты, энтропию, внутреннюю энергию через измеряемые величины — температуру, давление, объѐм и их производные.
Рассмотрим выражение для полн дифференциала внутрен энергии:

Известно, что если смешанные производные существуют и непрерывны, то они не зависят от порядка дифференцирования, то есть

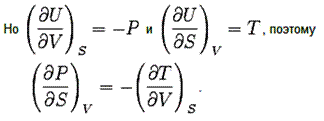
Рассматривая выражения для других дифференциалов, получаем:
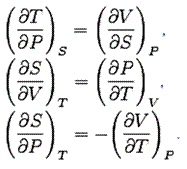
Эти соотношения называются соотношениями Максвелла.
Связь между термодинамическими потенциалами. Уравнение Гиббса-Гельмгольца Связь между внутренней энергией U и свободной энергией FТ.к.  а
а 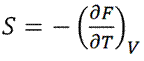 то
то 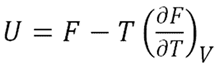
Поиск по сайту: