Напряженность поля точечного заряда

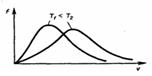
53. Изменение распределения Максвелла при изменении температуры газа. Вид распределения Максвелла в зависимости от молекулярной массы газа

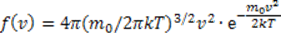
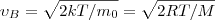(2)
Из формулы (2) мы видим, что при возрастании температуры максимум функции распределения молекул по скоростям (рис. 2) движется вправо (при этом становится больше значение наиболее вероятной скорости). Однако площадь, которая ограничена кривой, не меняется, поэтому кривая распределения молекул по скоростям при повышении температуры будет растягиваться и понижаться.

54. Время релаксации затухающих колебаний. Коэффициент затухания. Частота затухающих колебаний (формула).

Затухающие колебания- к-ия, энергия которых изменяется с течением времени t.

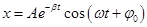- уравнение затухающих колебаний.

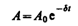— амплитуда затухающих колебаний, а А ₀ — начальная амплитуда.

Время релаксации — промежуток времени, в течение которого амплитуда затухающих колебаний уменьшается в е раз.

Коэффициент затухания – величина, обратно пропорциональная времени релаксации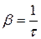

55. Барометрическая формула.

Выведем закон изменения давления с высотой, предполагая, что поле тяготения однородно, температура постоянна и масса всех молекул одинакова. Если атмосферное давление на высоте h равно p, то на высоте h+dh оно равно p+dp (при dh>0 dp<0, так как давление с высотой убывает). Разность давлений p и p+dp равна весу газа, заключенного в объеме цилиндра высотой dh с основанием площадью 1 м²: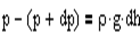

где - плотность газа на высоте h (dh настолько мало, что при изменении высоты в этом пределе плотность газа можно считать постоянной). Следовательно,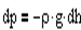

Воспользовавшись уравнением состояния идеального газа pV=(m/M)RT (m - масса газа, M - молярная масса газа), находим, что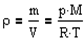

Подставим плотность и получим

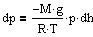à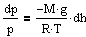

С изменением высоты от h₁ до h₂ давление изменяется от p₁ до p₂ т.е.

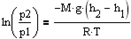à à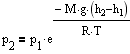

Выражение называется барометрической формулой. Она позволяет найти атмосферное давление в зависимости от высоты или, измерив давление, найти высоту. Так как высоты обозначаются относительно уровня моря, где давление считается нормальным, то выражение может быть записано в виде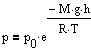

Барометрическую формулу можно преобразовать, если воспользоваться выражением p=nkT:

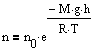
где n - концентрация молекул на высоте h, n₀ - то же, на высоте h=0. Так как M=m₀N_A ((N_A - постоянная Авогадро, m₀ - масса одной молекулы), а R=kN_A, то

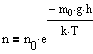где m₀gh= - потенциальная энергия молекулы в поле тяготения, т.е.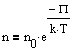

Полученное выражение называется распределением Больцмана для внешнего потенциального поля. Из него следует, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул. Если частицы имеют одинаковую массу и находятся в состоянии хаотического теплового движения, то распределения Больцмана справедливо в любом внешнем потенциальном поле, а не только в поле сил тяжести.

56. Разность потенциалов между двумя точками электростатического поля.

Так как потенциальная энергия , то работа сил поля равна:

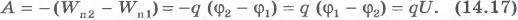
Здесь

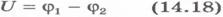
- разность потенциалов, т. е. разность значений потенциала в начальной и конечной точках траектории.
Разность потенциалов называют также напряжением.
Согласно формулам (14.17) и (14.18) разность потенциалов между двумя точками оказывается равной:

Разность потенциалов (напряжение) между двумя точками равна отношению работы поля при перемещении положительного заряда из начальной точки в конечную к величине этого заряда.
Если за нулевой уровень отсчета потенциала принять потенциал бесконечно удаленной точки поля, то потенциал в данной точке равен отношению работы электростатических сил по перемещению положительного заряда из данной точки в бесконечность к этому заряду.
Единица разности потенциалов. Единицу разности потенциалов устанавливают с помощью формулы (14.19). В Международной системе единиц работу выражают в джоулях, а заряд - в кулонах. Поэтому разность потенциалов между двумя точками численно равна единице, если при перемещении заряда в 1 Кл из одной точки в другую электрическое поле совершает работу в 1 Дж. Эту единицу называют вольтом (В); 1 В = 1 Дж/1 Кл.

Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциалов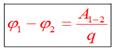

57. Первый закон термодинамики для изотермического и адиабатического процессов.

Согласно первому закону термодинамики, изменение внутренней энергии термодинамической системы при переходе из одного состояние в другое равно сумме работы, выполненной внешними силами, и количества теплоты, переданной системе извне

Сформулировать первый закон термодинамики можно иначе: количество теплоты, получаемое системой извне при ее переходе из одного состояния в другое, расходуется на повышение внутренней энергии системы и на работу, которую она выполняет против внешних сил

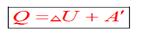
При изотермическом процессе температура не изменяется, значит не изменяется внутренняя энергия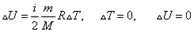

Первый закон принимает вид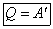

Все количество теплоты, которую получает газ расходуется на выполнение им работы против внешних сил. Или, если газ сжимается, при этом не изменяется температура, работу выполняют внешние силы, а газ отдает некоторое количество теплоты в окружающую среду.

В адиабатическом процессе Q = 0; поэтому первый закон термодинамики принимает вид

т. е. газ совершает работу за счет убыли его внутренней энергии.

58. Среднеквадратичная скорость. Наиболее вероятная скорость молекул.

Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью. Это скорость, вблизи которой на единичный интервал скоростей приходится наибольшее число молекул

Поиск по сайту: