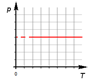
Уравнение изобарного процесса. Его график в координатах PV, PT, VT

Уравнение изобарного процесса для некоторого неизменного количества вещества ν имеет вид:

где V₀ – объем газа при температуре 0 °С. Коэффициент α равен (1/273,15) К^–1. Его называют температурным коэффициентом объемного расширения газов.

Изобарный процесс.

38. Потенциал электростатического поля, единицы измерения. Потенциал поля точечного заряда.

Потенциалом электростатического поля называется физическая величина, равная отношению потенциальной энергии заряда q_пр в данной точке пространства, к величине этого заряда

Потенциал поля точечного заряда Q: 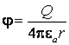_, где e₀-диэлектрическая постоянная 8,85*10^-12 Кл²/Н*м²
Потенциал измеряется в Вольтах=Дж/Кл

39. Адиабатический процесс. Уравнение Пуассона.

Адиабатическим называется процесс, при котором отсутствует теплообмен (δQ=0) между системой и окружающей средой. Адиабатическим процессами можно считать все быстропротекающие процессы. Таковым, например, можно считать процесс распространения звука в среде, так как скорость распространения звуковой волны настолько большая по значению, что обмен энергией между средой и волной произойти не успевает. Адиабатические процессы происходят в двигателях внутреннего сгорания (сжатие и расширение горючей смеси в цилиндрах), в холодильных установках и т. д.

первое начало термодинамики в этом случае приобретает вид

где — изменение внутренней энергии тела, — работа, совершаемая системой.
т. е. внешняя работа совершается за счет изменения внутренней энергии системы.
Используя формулы δA=pdV и C_V=dU_m/dT, для произвольной массы газа перепишем уравнение (1) в виде
(2)
применив дифференцирование уравнение состояния для идеального газа pV=(m/M)RT получим
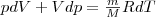(3)
Исключим из (2) и (3) температуру Т.

Разделив переменные и учитывая, что С_p/С_V=γ, найдем

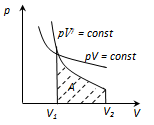
Проинтегрируя это уравнение в пределах от p₁ до p₂ и соответственно от V₁ до V₂, и потенцируя, придем к выражению
или
Так как состояния 1 и 2 выбраны произвольно, то можно записать (4)
Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.
безразмерная величина
(7)
называется показателем адиабаты (или коэффициентом Пуассона). Для одноатомных газов (Ne, He и др.), достаточно хорошо удовлетворяющих условию идеальности, i =3, γ=1,67. Для двухатомных газов (Н₂, N₂, О₂ и др.) i =5, γ=1,4.

40. Гармонические колебания. Амплитуда, фаза, циклическая частота гармонических колебаний, единицы измерения.

Гармоническое колебание -это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.

Уравнение гармонического колебания устанавливает зависимость координаты тела от времени.

Гармонические колебания величины s описываются уравнением типа где А — максимальное значение колеблющейся величины, называемое амплитудой колебания ( максимальное отклонение тела от положения равновесия),  ₀ — круговая (циклическая) частота ( число колебаний, совершаемых за 2π секунд ),  — начальная фаза колебания в мо­мент времени (это величина, которая определяет положение колебательной системы в любой момент времени) t= 0, ( ₀ t + ) — фаза колебания в момент времени t. Фаза колебания определяет значение колеблющейся величины в данный момент времени. Определенные состояния системы, совершающей гармонические колебания, повто­ряются через промежуток времени Т, называемый периодом колебания (в СИ в секундах), за который фаза колебания получает приращение 2 , откуда

Величина, обратная периоду колебаний, т. е. число полных колебаний, совершаемых в единицу времени, называется частотой колебаний.

Перемножив получим Это круговая циклическая частота (число колебаний, совершаемых за 2 π секунд).

Единица частоты — герц (Гц): 1 Гц — частота периодического процесса, при которой за 1 с совершается один цикл процесса.

41. Макроскопическая система. Что называется молем вещества? Молярная масса, число Авогадро, его величина и размерность.

Любой объект окружающего нас мира представляет собой совокупность из атомов.

Макроскопическая система – обобщенное название любого объекта в окружающем нас мире.

Параметры макроскопической системы – физические величины.

1. Количество вещества входящего в состав системы

- число Авогадро.

2. Объем

3. Температура – мера нагретости тела. Мера внутренней энергии макроскопической системы.

1. - объем макросистемы (тела) меняется от степени нагретости этого тела. Чем больше температура, тем больше объем.

2. При увеличении температуры, электрическое сопротивление тоже возрастает.

Уравнение Менделеева – Клапейрона.

- некие характерные моменты для вещества.

Первоначально возникла шкала Цельсия, потом шкала Фаренгейта, последней – шкала Кельвина.

4. Давление.

Количество структурных единиц, содержащихся в одном моле вещества определяет число Авогадро

Постоянная Авогадро N_A - число атомов, содержащихся в 12г изотопа углерода

1 Моль — это количество вещества, содержащее столько молекул, атомов, ионов, электронов или других структурных единиц, сколько содержится атомов в 12 граммах изотопа С (углерод)

Количество вещества - это отношение числа элементов этого вещества к постоянной Авогадро

1 моль любого вещества содержит одинаковое число частиц, это число равно постоянной Авогадро.

Молярная масса M - это масса одного моля вещества

Если тело состоит из N молекул массой m₀, то масса тела

42. Суммарное сопротивление последовательно включенных проводников. Суммарное сопротивление параллельно включенных проводников.

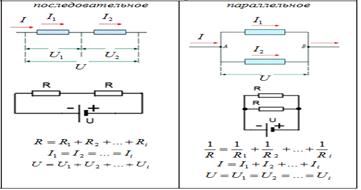
1.При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников

2.При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников

43. Уравнение Клапейрона - Менделеева. Физический смысл универсальной газовой постоянной.

Состояние данной массы газа полностью определено, если известны его давление, температура и объем. Эти величины называют параметрами состояния газа. Уравнение, связывающее параметры состояния, называют уравнением состояния.

Для произвольной массы газа состояние газа описывается уравнением Менделеева—Клапейрона: ,

где 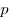— давление, — объем, — массa, - молярная масса, — универсальная газовая постоянная (). Физический смысл универсальной газовой постоянной в том, что она показывает, какую работу совершает один моль идеального газа при изобарном расширении при нагревании на 1 К.
Уравнение Менделеева—Клапейрона показывает, что возможно одновременное изменение трех параметров, характеризующих состояние идеального газа.

Изопроцессом называют процесс, происходящий с данной массой газа при одном постоянном параметре — температуре, давлении или объеме. Из уравнения состояния как частные случаи получаются законы для изопроцессов.

Изотермическим называют процесс, протекаю-щий при постоянной температуре: . Он описывается законом Бойля—Мариотта: .

Изохорным называют процесс, протекающий при постоянном объеме: . Для него справедлив закон Шарля: .

Изобарным называют процесс, протекающий при постоянном давлении. Уравнение этого процесса имеет вид при и называется законом Гей-Люссака. Все изопроцессы можно изобразить графически

44. Работа постоянного тока на участке цепи. Закон Джоуля - Ленца.

Работа тока- это работа электрического поля по переносу электрических зарядов вдоль проводника

Работа А электрического тока на участке цепи с электрическим сопротивлением R за время  t равна:

A = I · U ·  t = I^{2 ·} R ·  t

Формулой удобно пользоваться в случае последовательного соединения проводников, так как сила тока в этом случае одинакова во всех проводниках. При параллельном соединении удобна формула так как напряжение на всех проводниках одинаково.

Закон Дж-Ленца(Закон, определяющий количество теплоты, которое выделяет проводник с током в окружающую среду): Если на участке цепи не совершается механическая работа и ток не производит химического или иного действия, то вся работа тока затрачивается на нагревание проводника: А=Q

45. Идеальный газ. Основное уравнение молекулярно-кинетической теории идеального газа.

Идеальный газ

Это несуществующая физическая модель газа, который состоит из большого числа молекул, размеры которых ничтожно малы по сравнению со средними расстояниями между ними. Молекулы такого газа можно считать материальными точками, это означает, что их вращательное и колебательное движения не принимаются во внимание.

В молекулярно-кинетической теории пользуются идеализированной моделью идеального газа, согласно которому:
1.собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда

2.между молекулами газа отсутствуют силы взаимодействия

3.столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.

Для описания свойств газов можно пользоваться:

1. микроскопическими параметрами (скорость, масса молекулы, ее энергия и др.), которые являются характеристиками молекул и средние численные значения которых находятся только расчетным путем;

2. макроскопическими параметрами (давление, температура, объем газа), значение которых определяется совместным действием огромного числа молекул. Макропараметры — это параметры, характеризующие состояние системы (газа) в целом и не имеющие смысла в применении к отдельным частицам системы. Численные значения их находят измерением с помощью приборов и расчетным путем.

Давление газа p — это средняя сила ударов его молекул о тело (например, о стенки сосуда), отнесенная к единице поверхности тела.

Абсолютная температура T — мера средней кинетической энергии теплового движения молекулы (см. Температура и тепловое равновесие системы).

Под объемом газа V понимают внутренний объем сосуда, в котором находится газ.

Молекулярно-кинетическая теория:

Поиск по сайту: