 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ФормулаТорричелли

Рассмотрим два сечения (на уровне h1 и h2), напишем для них ур-е Бернулли:

 ,
,
Т.к. p1=p2=Атм., то: 
из ур-я неразрывности следует, что  ,
,
Если S1>>S2, то  , и членом
, и членом 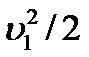 можно пренебречь:
можно пренебречь:

 ,
,
это выражение и есть формула Торричелли.
21. Внутреннее трение (вязкость). Режимы течения.
Вязкость – св-во реальных жидкостей оказывать сопротивление перемещению одной части жидкости относительно другой.
Градиент скорости – величина  показывает, как быстро меняется скорость при переходе от слоя к слою, в направлении перпендикулярном движению слоёв, т.о. сила трения:
показывает, как быстро меняется скорость при переходе от слоя к слою, в направлении перпендикулярном движению слоёв, т.о. сила трения:
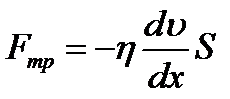 ,где вязкость – коэффициент пропорциональности, зависящий от природы жидкости.
,где вязкость – коэффициент пропорциональности, зависящий от природы жидкости.
Режимы течения:
1) Ламинарное – течение, при котором каждый выделенный тонкий слой скользит относительно соседних, не перемешиваясь с ними.

Это течение наблюдается при низких скоростях её движения.
2) Турбулентное – течение, при котором вдоль потока происходит интенсивное вихреобразование, и перемешивание жидкости.

Частицы жидкостей приобретают составляющие скоростей, перпендикулярны течению, поэтому они могут переходить из одного слоя в другой. Из-за большого градиента скоростей у поверхности трубы происходит образование вихрей.
Вязкость жидкости – перенос импульса между контактирующими слоями.  - кинематическая вязкость.
- кинематическая вязкость.

Re – число Рейнольдса, характер движения завит от него:
Re<=1000, то ламинарное
1000<=Re<=2000, переход от ламинарного к турбулентному.
Re=2300, то турбулентному
22. Метод Стокса.
Основан на измерении скорости медленно движущихся в жидкости небольших тел сферической формы.
На шарик, падающий в жидкости вертикально вниз, действуют 3 силы:
Сила тяжести:  (плотность шарика)
(плотность шарика)
Сила Архимеда:  (плотность жидкости)
(плотность жидкости)
Сила сопротивления (Стокса):.
При равномерном движении шарика:
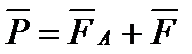 ,
,
проекции: 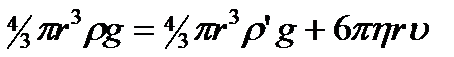
отсюда:
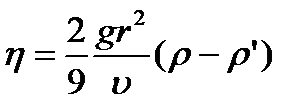
23. Метод Пуазейля.
Основан на ламинарном течении жидкости в тонком капилляре.
В жидкости мысленно выделим цилиндрический слой радиусом r и толщиной dr, сила внутреннего трения, действующая на боковую поверхность этого слоя равна:  ,
,
где dS – боковая поверхность, есть (-), т.к. при возрастании радиуса скорость уменьшается.
Сила вязкости уравновешивается силой давления, действующей на основание: 

 За время t из трубы вытечет жидкость объёмом:
За время t из трубы вытечет жидкость объёмом:




 .
.
24. Поверхностное натяжение.
Для жидкости характерен ближний порядок расположения частиц, т.е. их упорядоченное расположение, повторяющееся на расстояниях, сравнимых с межатомными.
Радиус молекулярного действия (r=10-9м) – С расстояния более этого радиуса силами межмолекулярного взаимодействия можно пренебречь.
Результирующие силы всех молекул поверхностного слоя оказывают на жидкость давление, называемое молекулярным, или внутренним.
У молекул на поверхности сущ-ет дополнительная П. энергия, называемая поверхностной энергией.  ,
,
где сигма – поверхностное натяжение.

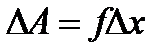 ,
,
где 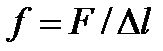 - сила поверхностного натяжения, действующая на единицу длины контура поверхности жидкости.
- сила поверхностного натяжения, действующая на единицу длины контура поверхности жидкости.  ,
,
эта работа совершается за счёт уменьшения поверхностной энергии, т.е.:


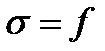 ,
,
т.е. поверхностное натяжение равно силе поверхностного натяжения, действующей на единицу длины контура поверхности жидкости.
Поверхностно-активные – в-ва, влияющие на поверхностное натяжение жидкости.
(мыло -  , соль/сахар -
, соль/сахар -  )
)
25. Смачивание и не смачивание.
Краевой угол – угол между касательными к поверхности жидкости и твёрдого тела.


Условие равновесия капли является равенство нулю суммы проекций сил поверхностного натяжения на направление касательной к поверхности твёрдого тела:  ;
;
 ,из этого условия следует, что:
,из этого условия следует, что:
смачивание

не смачивание

Условие равновесия жидкости:
 .
.
Полное смачивание:
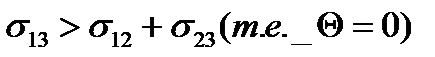
Полное не смачивание:

26. Давление под искривлённой поверхностью жидкости. Формула Лапласа.
Если поверхность жидкости не плоская, а искривленная, то она оказывает на жидкость избыточное (добавочное) давление, т.к. действуют силы поверхностного натяжения, для выпуклой поверхности положительно, а для вогнутой – отрицательно. 
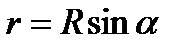 На каждый бесконечно малый элемент длины
На каждый бесконечно малый элемент длины 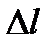 контура действует сила поверхностного натяжения:
контура действует сила поверхностного натяжения:  ,
,
касательная к поверхности сферы.
Разложив 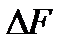 на две составляющие
на две составляющие 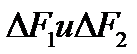 , видим, что геометрическая сумма сил
, видим, что геометрическая сумма сил 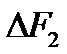 равна нулю, т.е. равнодействующая сил поверхностного натяжения, действующих на вырезанный сегмент, направлена перпендикулярно плоскости сечения. И равна:
равна нулю, т.е. равнодействующая сил поверхностного натяжения, действующих на вырезанный сегмент, направлена перпендикулярно плоскости сечения. И равна:


 Это и есть формула избыточного (добавочного) давления для выпуклой поверхности.
Это и есть формула избыточного (добавочного) давления для выпуклой поверхности.
Для вогнутой:
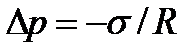 Эти две формулы являются частными случаями формулы Лапласа, определяющей избыточное давление для произвольной поверхности жидкости двоякой кривизны:
Эти две формулы являются частными случаями формулы Лапласа, определяющей избыточное давление для произвольной поверхности жидкости двоякой кривизны:  .
.
27. Капиллярные явления.
Капиллярность – явление изменения высоты жидкости в капиллярах.
жидкость в капилляре поднимается или отпускается на такую высоту h, при которой давление столба жидкости (гидростатическое давление)  уравновешивается избыточным давлением
уравновешивается избыточным давлением  , т.е.:
, т.е.:
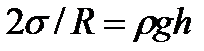 , т.к.
, т.к. 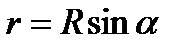 , то:
, то:
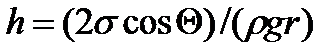
Поиск по сайту: