Преобразования Галлилея

Принцип относительности Галилея – во всех инерциальных системах отсчёта законы классической динамики имеют одинаковую форму.

Систма К’ движущаяся относительно К равномерно и прямолинейно со скоростью u (u=const). Скорость u направлена вдоль ОО’, радиус-вектор, проведённый из О в О’, .

Найдём связь между координтами произвольной точки А в обеих системах:

.

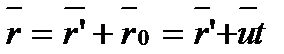Это уравнения преобразований координат Галилея.

В частном случае, когда система К’ движется со скоростью v вдоль положительного направления оси системы К:

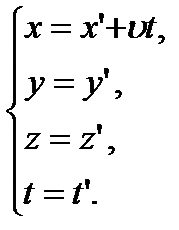
Соотношения справедливы при (u<<c):

.

Продифферинцировав получим уравнение:

,

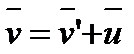которое представляет собой правило сложения скоростей в классической механике. Ускорение в системе отсчёта К:

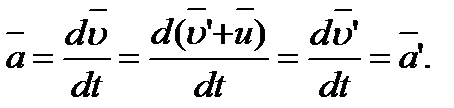
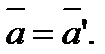
Следовательно, если на точку А другие тела не действуют (а =0), то, согласно (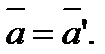), и а’ =0, т. е. система К’ является инерциальной (точка движется относительно неё равномерно и прямолинейно или покоится).

Таким образом, из соотношения 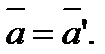вытекает доказательство механического принципа относительности: уравнения динамики при переходе от одной инерциальной системы отсчёта к другой не изменяется, т.е. являются инвариантными по отношению к преобразованиям координат.

Поиск по сайту: