 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Адгезия – притяжение частиц из разных фаз
 21 21
|
 31 31
|
 23 23
|
| Р и с. 2.4.1.1. К выводу соотношения между работой адгезии и поверхностными натяжениями взаимодействующих компонентов (уравнение Дюпре): 1 – газ; 2 – жидкость; 3 – твердое тело |
Чтобы получить соотношение между работой адгезии и поверхностным натяжением взаимодействующих компонентов, представим себе две конденсированные фазы 2 и 3, имеющие поверхность на границе с воздухом 1, равную единице площади (рис. 2.4.1.1).
Будем считать, что фазы взаимно нерастворимы. При совмещении этих поверхностей, т.е. при нанесении одного вещества на другое происходит явление адгезии, т.к. система стала двухфазной, то появляется межфазное натяжение s23. В результате первоначальная энергия Гиббса системы снижается на величину, равную работе адгезии:
 G + Wa=0, Wa= -
G + Wa=0, Wa= -  G.
G.
Изменение энергии Гиббса системы в процессе адгезии:
 ;
;
G нач. = s 31 + s 21;
Gкон = s23;
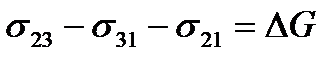 .
.
 - уравнение Дюпре.
- уравнение Дюпре.
Межфазное натяжение станет равно 0, когда исчезнет межфазная поверхность, что происходит при полном растворении фаз

Учитывая, что Wk=2s, и умножая правую часть на дробь  , получим:
, получим:

где Wk2, Wk3 - работа когезии фаз 2 и 3.
Смачивание - поверхностное явление, заключающееся во взаимодействии жидкого с твердым или другим жидким телом при наличии одновременного контакта трех несмешивающихся фаз, одна из которых обычно является газом.
 21 21
|
| s23 |
| s31 |
| Р и с. 2.4.1.2. Капля на поверхности твердого тела в условиях равновесия |
| q |
 - закон Юнга.
- закон Юнга.
Если cos q > 0, то поверхность хорошо смачивается этой жидкостью, если cos q < 0, то жидкость плохо смачивает это тело (кварц – вода – воздух: угол q = 0; «тефлон – вода – воздух»: угол q = 1080). С точки зрения смачиваемости различают гидрофильные и гидрофобные поверхности.
Если 0< угол q<90, то поверхность гидрофильная, если краевой угол смачиваемости q>90, то поверхность гидрофобная. Удобная для расчета величины работы адгезии формула получается в результате сочетания формулы Дюпре и закона Юнга:
 ;
;
 ;
;
 - уравнение Дюпре-Юнга.
- уравнение Дюпре-Юнга.
Из этого уравнения видна разница между явлениями адгезии и смачиваемости. Разделив обе части на 2, получим
 .
.
Так как смачивание количественно характеризуется cos q, то в соответствии с уравнением оно определяется отношением работы адгезии к работе когезии для смачивающей жидкости. Различие между адгезией и смачиванием в том, что смачивание имеет место при наличии контакта трех фаз. Из последнего уравнения можно сделать следующие выводы:
1. При q= 0 cos Q = 1, Wa=Wk.
2. При q = 900 cos q = 0, Wa=Wk/2.
3. При q =1800 cos q = -1, Wa=0.
Последнее соотношение не реализуется.
Рассмотрим условие растекания жидкости 2 по поверхности 3. Это условие можно получить из закона Юнга, приняв, что процесс проходит при q < 0. Тогда s31 ³ s23 + s21.
При этом условии равновесие становится невозможным и происходит растекание. Из уравнения следует, что уменьшение межфазного натяжения s23 и уменьшение поверхностного натяжения жидкости s21 способствует растеканию. Если разность s31 и s23 заменить выражением из уравнения Дюпре, что получим условие растекания в виде

Таким образом, растекание происходит в том случае, если работа адгезии превышает работу когезии растекания жидкости. Разницу между левой и правой частями неравенства называют коэффициентом растекания f или коэффициентом растекания по Гаркинсу.
 ;
;  .
.
При положительном значении коэффициента растекания жидкость растекается, при отрицательном - не растекается. Растекание жидкости с меньшим поверхностным натяжением по жидкости с бớльшим поверхностным натяжением называют эффектом Марангони.
Поиск по сайту: