 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Классификация по агрегатному состоянию фаз

Волан-де-Морт до Хогвартса
Волан-де-Морт родился полукровкой - его мать (Меропа Мракс) была волшебницей, а отец маглом (Том Реддл). Мать назвала будущего Темного Лорда в честь отца - Том и в честь деда с материнской стороны - Нарволо. Отец Волан-де-Морта, передавший ему свою красоту, бросил мать, как только узнал, что она колдунья и околовала его приворотным зельем. Мать с Томом на руках осталась без средств существования. Она продала последнюю свою ценную вещь - Медальон Слизерина за гроши. Мать просто не могла обеспечить Волан-де-Морту нормальную жизнь и оставила его в магловском приюте. До 11 лет юный Волан-де-Морт не знал, что он волшебник, но он замечал что владеет некоторыми необъяснимыми способностями и уже в таком возрасте умел использовать эти способности не во благо приюту и его обитателям. С помощью волшебства Волан-де-Морт запугивал, подчинял и наказывал других детей в приюте. Кроме этого Волан-де-Морт уже ребенком был очень властным, умным, умеющим добиваться, того чего хотел и единоличником. Волан-де-Морт ни с кем ничем не делился, любил все делать один и терпеть не мог походить на других, он хотел быть знаменитостью, особенным. В 11 лет к Волан-де-Морту пришел старый волшебник - Альбус Дамблдор и рассказал ему о том, кто он такой и пригласил в школу чародейства и волшебства, куда Волан-де-Морт с радостью пошел.
Волан-де-Морт в Хогвартсе
С 11 до 18 лет Волан-де-Морт 9 месяцев учился в Хогвартсе, а на летних каникулах жил в приюте. В Хогвартсе Волан-де-Морт и придумал себе это имя переставив буквы из слов Том Нарволо Реддл и получив слова Лорд Волан-де-Морт. В школе Волан-де-Морт всячески угождал учителям (например присылал засахаренные ананасы Слизнорту) и выручал из этого пользу (например узнавал тайные вершины Темной Магии). Также Волан-де-Морт уже в школе начал иметь что-то вроде верных прислужников. Например, таким был Антонин Долохов. Долго Волан-де-Морт искал в Хогвартсе Тайную Комнату, поскольку знал, что только наследник Слизерина может ее открыть. На пятом курсе Волан-де-Морт нашел эту комнату и выпустил василиска. Погибло много учеников, но Волан-де-Морту на это было наплевать. Волан-де-Морт закрыл комнату только тогда, когда Армандо Диппет сказал ему, что если нападения не прекратятся и преступник не будет пойман школу закроют. В такой ситуации Волан-де-Морт принял подлое решение: подставить третьекурсника Рубеуса Хагрида. Волан-де-Морт исполнил задуманное и Хагрида исключили из школы. Но чтобы вся работа (поиски Тайной комнаты) не прошла впустую Волан-де-Морт заключил свое 16-летнюю часть души в свой дневник. Это был первый крестраж Волан-де-Морта. На каникулах Волан-де-Морт оглушил своего дядю Морфина. Волан-де-Морт убил палочкой Морфина своего отца, дедушку и бабушку с отцовской стороны (по той причине, что они были маглами). Потом Волан-де-Морт пришел обратно в дом дяди украл перстень Нарволо и изменил память Морфину, чтобы вся вина пала на него (Морфин признался, что он убийца). Как и следовало ожидать Волан-де-Морт окончил Хогвартс с самыми высшими высшими оценками.
Волан-де-Морт до Падения
После того, как Волан-де-Морт закончил Хогвартс он сделал кольцо Нарволо вторым крестражем и спрятял в руинах дома Нарволо. Затем Волан-де-Морт пошел искать Диадему Когтевран в лесах Албании, нашел ее и сделал из нее третий крестраж. Волан-де-Морт пошел просить место преподавателя защиты от Темных искусств, но Армандо Диппет не взял его на работу во-первых потому что Том был слишком юн, а во-вторых его отговорил Дамблдор. Потом Волан-де-Морт устроился на работу в "Горбин и Беркес". Волан-де-Морт устроился на эту работу неслучайно - через этот магазин проходило много ценных вещей. Все преподаватели Хогвартса, думавшие, что он пойдет по стопам Министерства магии не могли поверить, что Волан-де-Морт при его-то знаниях устроился в какую-то лавчонку. Но Волан-де-Морт не был просто продавцом - также (из-за большого обаяния и умения обходиться с людьми Волан-де-Морта) его посылали уговаривать людей уступить свои сокровища магазину. Однажды Волан-де-Морта послали к Хепзибе Смит для того, чтобы она уступила магазину доспехи гоблинской работы. Но Волан-де-Морт так понравился Хепзибе своей пунктуальностью, красотой, лестью и обаянием, что Хепзиба решилась показать ему два своих самых заветных сокровища - Медальон Слизерина и Чашу Пуффендуй. Волан-де-Морт убил старуху, отобрал сокровища, из которых сделал свои третий и четвертый крестражи, изменил память домовому эльфу Похлебе и больше никогда не появлялся в лавке "Горбин и Беркес". По мере того, как Волан-де-Морт создавал все больше крестражей, он утрачивал красоту и человеческий облик - кожа становилась бледной, волосы начали выпадать, зрачки глаз краснели, нос становился змеиным, шелки ноздрей и разрез глаз сужался. Волан-де-Морт созвал всех прислужников, которые называли себя Пожирателями смерти, великанов и дементоров, которым обещал свободу в действиях. И вот Волан-де-Морт начал властвовать. Волан-де-Морт настолько сильно наводил страх на людей, что они боялись даже произнести его имя и называли его Тот-Кого-Нельзя-Называть, Сам-Знаешь-Кто, даже Пожиратели называли его Темный Лорд. Обдумав все, Волан-де-Морт в компании Пожирателей смерти пошел снова просить место преподавателя защиты от Темных искусств. Теперь директором был Дамблдор, и он опять отказал Волан-де-Морту поняв, что в его власти будет много учеников, если он станет преподавателем. Перед уходом из Хогвартса Волан-де-Морт спрятал в Выручай - комнате Диадему Когтевран. Потом Волан-де-Морт спрятал Медальон Слизерина в той самой пещере, в которой запугивал детей в детстве и окружил его магической защитой. А Чашу Пуффендуй отдал на хранение в Гринготтс в сейф Лестрейнджей. Война между Волан-де-Мортом, его слугами и Министерством магии длилась очень долго. Однажды Северус Снегг (один из Пожирателей) доложил Волан-де-Морту о части пророчества, которую успел подслушать. В ней говорилось о мальчике, способном ниспровергнуть Темного лорда. По описаниям подходило два мальчика - Невилл Долгопупс и Гарри Поттер. Волан-де-Морт выбрал Гарри Поттера - полукровку нежели чистокровного волшебника потому что заметил в Гарри себя еще даже не взглянув на него. Он убил его родителей, но не смог убить Гарри самого из-за того, что мать Гарри отдала жизнь ради него. Заклинание ударило рикошетом по Волан-де-Морту, но он остался жив из-за крестражей, созданных им.
Возрождение Волан-де-Морта
После падения Волан-де-Морт прятался в лесах Албании. Волан-де-Морт стал даже меньше, чем дух. Но Волан-де-Морт мог вселяться в людей и животных. Животные, в которых Волан-де-Морт вселялся (чаще всего в змей) быстро умирали. К тому же в облике животных Волан-де-Морт не мог колдовать. Поэтому Волан-де-Морту необходимо было вселиться в волшебника. Однажды в леса Албании забрел один доверчивый волшебник - Квиринус Квиррелл. Волан-де-Морт подчинил себе Квиррелла и приказал ему проникнуть в Гринготтс и украсть философский камень. Но Квиррелл опоздал, камень уже забрали из сейфа. Квиррелл привез Волан-де-Морта в Англию. Здесь Волан-де-Морт вселился в Квиринуса, чтобы лично контролировать его. Квиррелл был учителем в Хогвартсе, и философский камень был доставлен тоже в Хогвартс. Волан-де-Морт вместе с Квиринусом заколдовал метлу Гарри Поттера, чтобы убить его. Но Волан-де-Морту помешал Северус Снегг, который тоже теперь работал преподавателем в Хогвартсе. Снегг, как мог мешал Квирреллу и Волан-де-Морту заполучить философский камень. Но все-таки Волан-де-Морт забрался в хранилище философского камня и обошел все препятствия, кроме последнего. Волан-де-Морту снова помешал Гарри Поттер. Опять подействовала древняя магия матери Гарри. Как только Гарри и Квиринус соприкоснулись Квиррелл начал тлеть и превращаться в песок. Волан-де-Морту пришлось покинуть тело Квиррелла. Волан-де-Морт вернулся в леса Албании. Через два года к Волан-де-Морту пришел Питер Петтигрю вместе с Бертой Джоркинс. Волан-де-Морт с помощью легилименции выведал у Берты, что в этом году в Хогвартсе будет проводиться Турнир Трех Волшебников, и что еще остался верный и преданный Волан-де-Морту Пожиратель смерти - Бартемий Крауч младший. Теперь Берта не нужна была Волан-де-Морту и он ее убил. Волан-де-Морт создал последний крестраж - свою змею Нагайну. Вселиться в Питера Волан-де-Морт не мог, потому что он считался мертвым. Петтигрю, следуя указаниям Волан-де-Морта, помог ему вернуться в почти человеческий облик, используя заклинания, изобретенные Волан-де-Мортом и зелье, сваренное из крови единорога и яда Нагайны. В этом облике Волан-де-Морт пришел домой к преданному Пожирателю смерти. Волан-де-Морт подверг заклятию Империус Крауча старшего и приказал ему отправлять письма в Министерство будто он болеет. А Пожирателю Волан-де-Морт приказал отправляться в Хогвартс, пить Оборотное зелье и прикидаваться Аластором Грюмом. Но однажды Крауч старший очнулся от заклятия Волан-де-Морта и сбежал в Хогвартс, чтобы сообщить обо всем Дамблдору. Волан-де-Морт сразу оповестил Крауча младшего и он убил своего отца. Потом Волан-де-Морт велел Барти превратить кубок в портал. А сам Волан-де-Морт пришел на руках у Хвоста на кладбище. Кубок перенес на кладбище Гарри и Седрика. Волан-де-Морт приказал Хвосту убить Седрика и привязать Гарри к надгробью. Затем Хвост опустил в котел, который притащил заранее, тело Волан-де-Морта, кость его отца, свою отрезанную руку и кровь Гарри. И вот Волан-де-Морт с человеческим телом вышел из котла. Тут же Волан-де-Морт созвал всех Пожирателей смерти. Также Волан-де-Морт подарил Хвосту новую серебряную руку. Затем Волан-де-Морт вызвал Гарри на дуэль. Их заклинания - Авада Кедавра и Экспеллиармус - столкнулись и из палочки Волан-де-Морта начали выходить все его жертвы. Жертвы окружили Волан-де-Морта закрывая от него Гарри. А Гарри тем временем схватил тело Седрика и снова схватился за кубок, который отнес его обратно в Хогвартс, таким образом Волан-де-Морт снова не смог убить Гарри.
Пророчество Волан-де-Морта
После побега Гарри у Волан-де-Морта появилась цель - прослушать пророчество целиком. Запись пророчества находилась в Отделе тайн (в одном из Министерских отделов). Волан-де-Морт посылал туда много людей. Все люди Волан-де-Морта либо вообще не доходили до цели, либо сходили с ума. Потом Волан-де-Морт вселился в свою змею Нагайну. Волан-де-Морт смог доползти только до двери в Отдел тайн, потому что дверь охранял Артур Уизли. Волан-де-Морт покусал его и уполз обратно - слишком долго задерживаться нельзя - вдруг кто нагрянет. Волан-де-Морт понял, что взять пророчество и не сойти с ума могут только те, к кому оно относится. Сам Волан-де-Морт в Министерство прийти не мог, поэтому думал как заманить туда Гарри. Еще Волан-де-Морт узнал, что между ним и Гарри существует связь, которая позволяет им входить в сознание друг другу. Волан-де-Морт попытался с помощью этой связи завладеть Гарри, но испытал такую боль, что больше не пытался этого сделать. Однажды к Беллатрисе Лестрейндж (одной из верных слуг Волан-де-Морта) пришел ее бывший домовой эльф Кикимер и рассказал ей, что Сириус Блэк стал для Гарри кем-то вроде отца и то, что Гарри ради него все сделает. Беллатриса тут-же сообщила об этом Волан-де-Морту. А Волан-де-Морт представил, что пытает Сириуса в Отделе тайн, и приказал Люциусу Малфою возглавлять других Пожирателей, пока они будут отбирать пророчество у Гарри. Как и думал Волан-де-Морт Гарри вместе с друзьями примчался в Отдел тайн. Но у Пожирателей не получилось отобрать пророчество про Гарри и Волан-де-Морта. Оно разбилось. Тогда Волан-де-Морт лично пришел в Отдел тайн и сразился с Дамблдором. Потом в Отдел тайн нагрянули Министерские работники и сам министр Корнелиус Фадж, а Волан-де-Морт трансгессировал.
Вторая война
Волан-де-Морт приказал захватить в плен Олливандера. А Олливандеру приказал сделать новую палочку Питеру Петтигрю. Волан-де-Морт спросил у Олливандера почему он не смог убить мальчишку три года назад. Олливандер ответил Волан-де-Морту, что его палочка и палочка Гарри сестры - сделаны из пера одного и того же феникса Фоукса. Разгневавшись на Люциуса за то, что он провалил операцию с пророчеством, Волан-де-Морт дал невыполнимый приказ его сыну Драко убить Дамблдора. Но Дамблдора был убит хоть и не Драко, а Снеггом. В предыдущем году к Волан-де-Морту снова пришли великаны и дементоры, поэтому он с легкостью совершил массовый побег преданных ему Пожирателей смерти. После того, как Люциус сбежал из Азкабана вместе с другими Пожирателями Волан-де-Морт попросил у него палочку, чтобы избежать влияние палочки-сестры. Со своим возрождением Волан-де-Морт начал совершенствовать свою магию и научился самостоятельно летать. Северус Снегг доложил Волан-де-Морту, что Гарри Поттер будет перевозиться в субботу при наступлении вечера. Волан-де-Морт и Пожиратели устроили засаду, но они не знали, что Орден Феникса устроил идею семерых Поттеров. Волан-де-Морт наивно подумал, что Гарри будет лететь с самым опытным мракоборцем Грозным Глазом и первым взялся за него. Но когда поддельный Гарри трансгрессировал от заклинания и оно попало в Грюма, Волан-де-Морт понял, что ошибся. Дальше он взялся за Кингсли Брувстера, но его позвали Пожиратели и Волан-де-Морт помчался за настоящим Гарри. Ему осталось совсем чуть-чуть, чтобы выкрикнуть заклинание и убить Гарри, но палочка Гарри самостоятельно уничтожила палочку Люциуса невероятно мощным заклинанием. Не успел Волан-де-Морт попросить палочку у другого Пожирателя, как Гарри перелетел магическую защиту Министерства и Ордена. После этого случая Волан-де-Морт начал пытать Олливандера и спрашивать почему палочка Гарри уничтожила одолженную, но тот ничего не знал. Заодно Волан-де-Морт расспросил Олливандера про Бузинную палочку, на что Олливандер ответил, что слышал, как Грегорович хвастался ею. Волан-де-Морт полетел к Грегоровичу, он нашел его и начал расспрашивать о Бузинной палочке. Он узнал, что палочку украл какой-то юноша и убил Грегоровича. Волан-де-Морт несмотря на то, что все знали про его возрождение не действовал открыто. Благодаря этому начали распространяться слухи о том, что Волан-де-Морт может убить взглядом, таким образом волшебный народ был сльно запуган. Кроме того, чтобы поймать врагов Волан-де-Морта на его имя наложили Табу, то есть каждого, произнесшего слово "Волан-де-Морт" ловили Пожиратели.
Волан-де-Морт на всякий случай оставил в Годриковой впадине змею Нагайну, которая была заключена в тело Батильды Бэгшот с помощью Темной магии. Однажды Нагайна вызвала Волан-де-Морта так как нашла Гарри Поттера. Волан-де-Морт быстро примчался, но Гарри и Гермиона успели прыгнуть в окно и трансгрессировать. Несмотря на неудачу, Волан-де-Морт не зря прибыл в дом Батильды - здесь он нашел на полу фотографию молодого вора Бузинной палочки. Это был Геллерт Грин-де-Вальд. Волан-де-Морт полетел в Нурменгард, тюрьму, в которой сидел Грин-де-Вальд. Грин-де-Вальд не хотел рассказывать ничего о палочке и поэтому Волан-де-Морту пришлось убить его. Пожиратели смерти вызвали Волан-де-Морта с помощью Черной Метки в особняк Малфоев, так как схватили Поттера. Но когда Волан-де-Морт прибыл в особняк, Гарри и его друзья снова сбежали. Волан-де-Морт наказал Пожирателей смерти за это. Раз у Грин-де-Вальда палочки не оказалось, то нужно поискать ее у его победителя - Дамблдора - решил Волан-де-Морт. Волан-де-Морт прибыл в Хогвартс, разрушил гробницу Дамблдора и взял оттуда Бузинную палочку. Через некоторое время Волан-де-Морту доложили, что из сейфа Лестрейнджей Гарри Поттером была украдена Чаша Пуффендуй. Волан-де-Морт понял, что Гарри охотится за крестражами и начал проверять свои тайники. Медальон, Кольцо, Дневник, Чаша к этому времени были уже уничтожены. У Волан-де-Морта остались три крестража: Диадема, Нагайна и Гарри Поттер (он невольно сделал его своим крестражем). Чтобы Гарри не добрался до оставшихся крестражей он предупредил Снегга и Кэрроу, что Гарри может явиться в Хогвартс, в башню Когтеврана и окружил Нагайну волшебной защитой. Волан-де-Морт узнал, что Гарри Поттер внутри Хогвартса и поэтому прилетел в Хогвартс и начал брать Хогвартс с боем. На стороне Волан-де-Морта были великаны, дементоры и большое количество Пожирателей смерти. До начала битвы Волан-де-Морт предупредил, что если они не выдадут Гарри Поттера, то начнется война. Во время битвы Волан-де-Морт приказал позвать Снегга. Северус явился и был убит змеей Волан-де-Морта, так как он думал, что раз Снегг убил Дамблдора, то Бузинная палочка теперь принадлежит ему. После больших потерь противников Волан-де-Морта он объявил защитникам Хогвартса, что они все будут убиты, если до 12 часов Гарри Поттер не придет к нему в Запретный лес. Волан-де-Морт уже отчаялся, что Гарри придет и тут он наконец прибыл. Волан-де-Морт применил к несопротивляющемуся Поттеру Авада Кедавра и думал, что убил его. Волан-де-Морт попросил проверить жив ли Гарри. Нарцисса проверила и соврала Волан-де-Морту. Волан-де-Морт с телом Гарри и Пожирателями смерти пришел в Хогвартс и сказал защитникам Хогвартса, что Гарри Поттер был убит при попытке бегства, большое количество защитников убито и сражаться теперь бесполезно. Но Невилл Долгопупс попытался послать заклятие в Волан-де-Морта. Волан-де-Морт его с легкостью отразил, обездвижил Долгопупса и одел ему на голову заженную Распределяющюю шляпу. Тут к защитникам Хогвартса подоспела подмога и начала истреблять Пожирателей: кентавры посылали стрелы в Пожирателей, великан Грохх молотил кулаками других великанов в то время как у них же выклевывали глаза фестралы и гиппогриф Клювокрыл, а домовые эльфы во главе с Кикимером вкалывали в щиколотки Пожирателям кухонные ножи и топоры. Волан-де-Морт отвлекся и Долгопупс выхватив из Распределяющей шляпы меч Годрика Гриффиндора отрубил голову Нагайне. Таким образом у Волан-де-Морта не осталось крестражей. Волан-де-Морт в ярости крушил и убивал всех, кто попадался ему на пути. Волан-де-Морт сражался сразу с тремя волшебниками Минервой МакГонангалл, Горацием Слизнортом и Кингсли Брувстером. Увидев, как Беллатриса умерла от руки Молли Уизли, Волан-де-Морт одним заклинанием побросал всех трех противников и уже хотел было послать заклинание в Молли, как Гарри Поттер разделил Большой зал Щитовыми чарами и отгородил Волан-де-Морта от Молли. Он все-таки остался жив.
Смерть Волан-де-Морта
В разговоре Гарри поведал Волан-де-Морту, что Северус Снегг работал на Дамблдора и убил его по приказу, а Бузинная палочка после смерти Дамблдора стала принадлежать Драко Малфою, но Гарри отвоевал палочку в честном бою у Драко и теперь Бузинная палочка принадлежала ему. Волан-де-Морт послал в Гарри Убивающее заклятие, а Гарри послал в него Обезоруживающее заклятие. В итоге все заклинания попали в Волан-де-Морта и он умер.
Классификация по агрегатному состоянию фаз
| Агрегатное состояние дисперсной фазы | Агрегатное состояние дисперсион-ной среды | Условное обозначе-ние фаза/среда | Название системы | Примеры |
| г | г | г/г ж/г тв/г | Аэрозоли | атмосфера Земли |
| ж | г | туман, слоистые облака | ||
| тв | г | дымы, пыли, перистые облака | ||
| г | ж | г/ж | Газовые эму-льсии, пены | газированная вода, мыльная и пивная пены |
| ж | ж | ж/ж | Эмульсии | молоко, масло сливочное, кремы и т.д. |
| тв | ж | тв/ж | Лиозоли, суспензии | лиофобные коллоидные растворы, суспензии, пасты, краски и т.д. |
| г | тв | г/тв | Твердые пены | пемза, пенопласт, активированный уголь, хлеб, пенобетон и т.д. |
| ж | тв | ж/тв | Твердые эмульсии | вода в парафине, минералы с жидкими включениями, пористые тела в жидкости |
| тв | тв | тв/тв | Твердые золи | сталь, чугун, цветные стекла, драгоценные камни |
Способы диспергирования заключаются в раздроблении тела до частиц дисперсных размеров.
Физико-химическое дробление (пептизация) представляет собой распад материала на более мелкие агрегаты под влиянием дисперсионной среды с образованием на частицах двойного электрического слоя.
Способы конденсации заключаются в укрупнении частиц, атомов, молекул до частиц дисперсных размеров (химическая реакция с образованием осадка).
Физическая конденсация из паров наблюдается при изменении параметров системы (температуры, давления и пр.), возникает новая фаза, система становится гетерогенной.
Физическая конденсация методом замены растворителя осуществляется при условии, когда изменение параметров системы вызывает превышение химического потенциала компонента в дисперсионной среде над равновесным химическим потенциалом, что приводит к образованию в системе новой фазы. В отличие от конденсации из паров, в данном методе используется изменение дисперсионной среды. В насыщенный истинный раствор вещества добавляют растворитель, в котором это вещество нерастворимо. Образуется пересыщенный раствор вещества в двух растворителях, где вещество агрегируется с образованием частиц новой дисперсной фазы.
При химической конденсации вещество новой фазы образуется в результате химической реакции.
Все молекулярно-кинетические свойства вызваны хаотическим тепловым движением молекул дисперсионной среды, которое складывается из поступательного, вращательного и колебательного движения молекул.
Молекулы жидкой и газообразной дисперсионной среды находятся в постоянном движении и сталкиваются между собой. Среднее расстояние, проходимое молекулой до столкновения с соседней, называют средней длиной свободного пробега. Молекулы обладают различной кинетической энергией. При данной температуре среднее значение кинетической энергии молекул остается постоянным, составляя для одной молекулы и одного моля:
 ;
;  ,
,
где m – масса одной молекулы;
M – масса одного моля;
v – скорость движения молекул;
k – константа Больцмана;
R – универсальная газовая постоянная.
Причина молекулярно-кинетических свойств - флуктуация (т.е. отклонение от среднего) значений кинетической энергии молекул дисперсионной среды.
Непрерывное, хаотическое, равновероятное для всех направлений движение мелких частиц, взвешенных в жидкостях или газах, за счет воздействия молекул
| F |
| х |
Определили эти изменения и связали их с молекулярно-кинетическими свойствами среды в 1907 году А. Эйнштейн и М. Смолуховский. В основе расчета – не истинный путь частицы дисперсной фазы, а сдвиг частиц. Если путь частицы определяется ломаной линией, то сдвиг х характеризует изменение координат частицы за определенный отрезок времени. Средний сдвиг определяет среднеквадратичное смещение частицы:
 ,
,
где х 1, х 2, хi – сдвиг частиц за определенное время.
После интегрирования этого уравнения при условии, что среднее произведение импульсов случайной силы равно нулю, среднее значение флуктуации (средний сдвиг) равно:
 ,
,
где t - время;
r – радиус частиц дисперсной фазы;
N A – число Авогадро частиц.
В этой формуле  характеризует молекулярно-кинетические свойства дисперсионной среды, h - ее вязкость, r – радиус частиц – параметр, относящийся к дисперсной фазе, а время t определяет взаимодействие дисперсионной среды с дисперсной фазой.
характеризует молекулярно-кинетические свойства дисперсионной среды, h - ее вязкость, r – радиус частиц – параметр, относящийся к дисперсной фазе, а время t определяет взаимодействие дисперсионной среды с дисперсной фазой.
Диффузией называют самопроизвольное распространение вещества из области с бόльшей концентрацией в область с меньшей концентрацией.
Диффузия высокодисперсных коллоидных частиц показана на рис. 1.1.2.1. В нижней части концентрация частиц больше, чем в верхней, т.е. v 1> v 2 (где
 , м3 – численная концентрация частиц, N – число частиц дисперсной фазы, V д.с. – объем дисперсной системы). Диффузия направлена из области с большей концентрации в область с меньшей концентрацией, т.е. слева направо (на рис. показано стрелкой). Диффузия характеризуется определенной скоростью перемещения вещества через поперечное сечение В, которая равна
, м3 – численная концентрация частиц, N – число частиц дисперсной фазы, V д.с. – объем дисперсной системы). Диффузия направлена из области с большей концентрации в область с меньшей концентрацией, т.е. слева направо (на рис. показано стрелкой). Диффузия характеризуется определенной скоростью перемещения вещества через поперечное сечение В, которая равна  .
.
На расстоянии D х разность концентраций составит v 2– v 1, т к. v 1> v 2, эта величина отрицательна. Изменение концентрации, отнесенное к единице расстояния, называют градиентом концентрации  или
или  .
.

- основное уравнение диффузии в дифференциальной форме
Скорость диффузии  величина положительная, а градиент концентрации
величина положительная, а градиент концентрации  - отрицателен, поэтому перед правой частью уравнения – знак «минус». Коэффициент пропорциональности D – это коэффициент диффузии. Основное уравнение справедливо для всех видов диффузии, в т.ч. и для коллоидных частиц. В интегральной форме оно применимо для двух процессов – стационарного и нестационарного:
- отрицателен, поэтому перед правой частью уравнения – знак «минус». Коэффициент пропорциональности D – это коэффициент диффузии. Основное уравнение справедливо для всех видов диффузии, в т.ч. и для коллоидных частиц. В интегральной форме оно применимо для двух процессов – стационарного и нестационарного:
1) для стационарного процесса:  =const. Значительное число диффузионных процессов близко к стационарным. Интегрируя
=const. Значительное число диффузионных процессов близко к стационарным. Интегрируя  , получим:
, получим:
 ;
;
 - I закон диффузии Фика
- I закон диффузии Фика
2) для нестационарного процесса:  ¹ const. Тогда интегрирование основного уравнения с учетом изменения градиента концентрации усложняется. При отсутствии в среде градиентов температуры, давления, электрического потенциала из уравнения
¹ const. Тогда интегрирование основного уравнения с учетом изменения градиента концентрации усложняется. При отсутствии в среде градиентов температуры, давления, электрического потенциала из уравнения  определим массу вещества m1, переносимого в результате диффузии в единицу времени через единицу площади поверхности, перпендикулярной направлению переноса (В = 1 и t = 1):
определим массу вещества m1, переносимого в результате диффузии в единицу времени через единицу площади поверхности, перпендикулярной направлению переноса (В = 1 и t = 1):  , с учетом которого можно определить пространственно-временное распределение концентрации:
, с учетом которого можно определить пространственно-временное распределение концентрации:
 - II закон диффузии Фика
- II закон диффузии Фика
Количественно диффузия определяется коэффициентом диффузии D, связанным со средним сдвигом соотношением:
 ;
;
 - продолжительность диффузии.
- продолжительность диффузии.
При разделении двух растворов различной концентрации или раствора и чистого растворителя полупроницаемой перегородкой (мембраной) возникает поток растворителя от меньшей концентрации к большей, выравнивающей концентрацию. Этот процесс называется осмосом.
На схеме (рис. 1.2.3.1) в сосуд с полупроницаемой перегородкой 3, помещен раствор 1. Перегородка пропускает дисперсионную среду (растворитель), но является препятствием для коллоидных частиц (растворенных веществ). Снаружи перегородки – чистый растворитель 2. Концентрация раствора по обе стороны перегородки различна. Внутри сосуда 1 часть раствора занимают молекулы растворенного вещества (частицы дисперсной фазы) Þ концентрация растворителя там меньше, чем в емкости 2 с чистым растворителем.
| m1 |
| m2 |
| Р и с. 1.2.3.1. Схема ос-моса: 1 – сосуд с раство-ром; 2 – емкость с раствори-телем; 3 – полупроницаемая мембрана |
| p, Н |
С термодинамической точки зрения, химический потенциал m2 чистой жидкости больше m1 растворителя в растворе, процесс самопроизвольно идет в сторону меньшего химического потенциала до их выравнивания: m2 = m1.
В результате перемещения жидкости в емкости 1 создается избыточное давление p, называемое осмотическим. Растворитель, проникающий в область раствора 1, поднимает уровень жидкости на высоту Н, что компенсирует давление чистого растворителя в сторону раствора. Наступает момент, когда вес столба жидкости в области раствора уравнивается давлением растворителя.
Осмотическое давление – такое избыточное давление над раствором, которое необходимо для исключения переноса растворителя через мембрану. Осмотическое давление равно тому давлению, которое производила бы дисперсная фаза (растворенное вещество), если бы она в виде газа при той же температуре занимала тот же объем, что и коллоидная система (раствор)
Осмотическое давление p достаточно разбавленных коллоидных растворов может быть найдено по уравнению:
 или
или  - уравнение Вант-Гоффа
- уравнение Вант-Гоффа
где mобщ/m – масса растворенного вещества;
m – масса одной частицы;
V – объем частицы;
NA – число Авогадро;
Т – абсолютная температура; n - частичная концентрация;
k – постоянная Больцмана;
М – масса одного моля растворенного вещества;
с – массовая концентрация. [2]
Оптические свойства дисперсных систем обусловлены взаимодействием электромагнитного излучения, обладающего определенной энергией, с частицами дисперсной фазы. Особенности оптических свойств дисперсных систем определяются природой частиц, их размерами, соотношением между длиной волны электромагнитного излучения и размерами частиц. При прохождении луча света через дисперсную систему могут наблюдаться следующие явления:
1. Преломление света частицами дисперсной фазы;
2. Отражение света частицами дисперсной фазы;
3. Светорассеяние (опалесценция);
4. Поглощение света.
Одним из характерных оптических свойств дисперсных систем является рассеяние света. В результате рассеяния проходящий через коллоидный раствор луч света становится видимым (эффект Тиндаля – рис. 1.3.1.1.) - опалесценция (в молекулярных и ионных растворах этот эффект не наблюдается).
Способностью к светорассеянию обладают не только частицы, но и ассоциаты молекул, макромолекулы, включения, нарушающие однородность среды. Рассеяние заключается в преобразовании веществом света, которое сопровождается изменением направления света. Схематически процесс рассеяния света выглядит так:
| Падающий свет с частотой n |
| Молекулы высокодисперсных частиц (атомы) |
| Поляризация молекул (атомов) и возникновение диполей с переменным моментом |
| + |
| ® |
| Падающий свет с частотой n1 |
| ® |
Световая волна вызывает поляризацию молекул, не проводящих и не поглощающих свет частиц, возникающий при этом дипольный момент определяется по уравнению: m = a Е, где a - поляризуемость; Е – напряженность возбужденного электрического поля, образованного падающим светом. Возникающие диполи колеблются с частотой падающего света и создают вторичное излучение во всех направлениях. В однородной среде свет, излучаемый всеми диполями вследствие интерференции, распространяется прямолинейно. В неоднородной среде, к которым относятся высокодисперсные системы с различным показателем преломления фазы и среды, интерференция отсутствует, и испускается некомпенсированное излучение в виде рассеянного света. Если энергия поглощенного кванта света (h n) равна энергии испускаемого кванта (h n1), то рассеяние будет рэлеевским (упругим). Оно реализуется, когда размеры частиц дисперсной фазы намного меньше длины волны света l:
а < 0,1l.
Длина волны видимого света колеблется в пределах 380 – 760 нм Þ условие справедливо для высокодисперсной фазы.
Светорассеяние наблюдается лишь тогда, когда длина световой волны больше размера частицы дисперсной фазы, т. е., lсв.в.>>ад.ф., а расстояние между частицами больше lсв.в. Если lсв.в.<< ад.ф. происходит отражение света, проявляющееся в мутности. Различают светорассеяние частицами, проводящими и непроводящими ток.
В результате рассеяния интенсивность падающего света I 0 изменяется и будет характеризоваться величиной I р, которая определяется по уравнению Рэлея:
 , (1.2.9)
, (1.2.9)
где v ч – численная концентрация дисперсной фазы;
V – объем частиц (для шарообразной частицы равный 4pr3/3);
r – радиус частицы;
l - длина волны падающего света;
n 1, n 2 – показатели преломления дисперсной фазы и дисперсионной среды.
Рэлеевское светорассеяние характерно для неэлектропроводных, оптически однородных и прозрачных частиц («белые золи»).
Оптические методы являются наиболее распространенными методами определения размера, формы и структуры коллоидных частиц. Наиболее часто для исследования коллоидных растворов применяются:
· ультрамикроскопия;
· электронная микроскопия;
· нефелометрия;
· турбидиметрия.
На границе раздела фаз существует избыток свободной энергии. Процесс увеличения площади поверхности при постоянном объеме выводит молекулы из глубины фазы на поверхностный слой, совершая при этом работу против межмолекулярных сил. Эта работа в изотермических условиях равна увеличению свободной поверхностной энергии. Для описания термодинамики поверхностных явлений используют два метода:
1. Метод избыточных величин Гиббса.
2. Метод слоя конечной толщины.
За толщину поверхностного слоя принимаем расстояние по обе стороны границы раздела фаз, за пределами которого свойства слоя перестают отличаться от свойств фазы в объеме.
| II |
| D Gсл |
 G2 ’ G2 ’
|
 G1 ’ G1 ’
|
| I |
| Р и с. 2.1.1.1. Сравнение термодинамических методов избыточных величин Гиббса (I) и «слоя конечной тол-щины» (II) |
| s, S |
| Фаза 2 |
 G1 G1
|
 G2 G2
|
| Фаза 1 |
 G 2 и поверхностной энергии Гиббса
G 2 и поверхностной энергии Гиббса  × B, которая является избыточной.
× B, которая является избыточной.

В методе слоя конечной толщины рассматривается поверхностный слой, имеющий определенные размеры (позиция II на рис. 2.1.1.1). Его термодинамические параметры включают как поверхностную энергию, так и энергию объема слоя, имеющего те же свойства, что и объемная фаза. Этот метод не рассматриваем. В методе Гиббса все экстенсивные величины выражаются в виде избытков по сравнению со значением этих величин в реальных объемных фазах.
На образование гетерогенной системы затрачивается работа
 ,
,
где s -коэффициент пропорциональности; B - новая поверхность.
Из объединенного уравнения первого и второго начал термодинамики для гетерогенной системы относительно изменения внутренней энергии выразим:
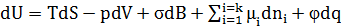
Но  , и для других термодинамических потенциалов:
, и для других термодинамических потенциалов:
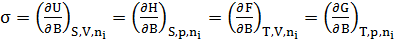 ,
,
Т.е. поверхностное натяжение – частная производная от любого термодинамического потенциала по площади межфазной поверхности при постоянстве соответствующих параметров.
Если проводить процесс образования новой поверхности изотермически и обратимо, то вся работа перейдет в запас свободной энергии поверхности:  ,
,  ;
;  , [Дж/м2 или Н/м].
, [Дж/м2 или Н/м].
Коэффициент s - поверхностное натяжение; s - это работа, совершаемая для образования единицы новой поверхности.
Поверхностное натяжение - это сила, действующая на единицу длины контура, ограниченного единицей поверхности и направленная в сторону сокращения поверхности, перпендикулярно к контуру вовнутрь его (рис. 2.1.2.1).
Поверхностное натяжение индивидуальных веществ (жидкостей) монотонно убывает с возрастанием температуры.
 Т=
Т=  - a
- a  T,
T,
где  Т - поверхностное натяжение при данной температуре;
Т - поверхностное натяжение при данной температуре;
 0 - поверхностное натяжение при стандартной температуре;
0 - поверхностное натяжение при стандартной температуре;
DТ - разность температур;
а - температурный коэффициент поверхностного натяжения;  ,
,  .
.
| 1 - ПАВ |
| 2 - поверхностно-инактивные вещества |
| 3 - индифферентные вещества |
| s |
| С |
| Р и с. 2.1.2.3. Характер зависимости поверхностного натяжения от концентрации вещества |
 = f(c) используется уравнение Шишковского:
= f(c) используется уравнение Шишковского:
 ,
,
где s0 – поверхностное натяжение растворителя (Н/м);
c – концентрация поверхностно-активного вещества (ПАВ);
А, K – константы:  ; K –константа адсорбционного равновесия из уравнения Ленгмюра.
; K –константа адсорбционного равновесия из уравнения Ленгмюра.
Запишем известное из термодинамики выражение внутренней энергии для поверхности.
 UВ =
UВ =  GВ + T
GВ + T  SВ - уравнение полной поверхностной энергии.
SВ - уравнение полной поверхностной энергии.
 - уравнение Гиббса - Гельмгольца для полной поверхностной энергии.
- уравнение Гиббса - Гельмгольца для полной поверхностной энергии.
Адсорбция - процесс самопроизвольного перераспределения компонентов системы между поверхностным слоем и объемом фазы.
Вещество, на поверхности которого происходит адсорбция, называется адсорбентом, а вещество, которое перераспределяется – адсорбатом.
Обратный процесс перехода вещества с поверхности в объем фазы - десорбция.
В зависимости от агрегатного состояния фаз различают адсорбцию газа на твердых адсорбентах, твердое тело – жидкость, жидкость - жидкость, жидкость - газ. Для количественного описания адсорбции применяют две величины:
1) Абсолютная адсорбция – это количество адсорбата, приходящееся на единицу поверхности адсорбента:
 ,
,
где n - число молей вещества в растворе;
В – площадь поверхности;
CB – концентрация адсорбата в поверхностном слое;
h – толщина слоя.
2) Величина, определяемая избытком вещества в поверхностном слое, отнесенным к единице площади поверхности или массы адсорбента, называется Гиббсовской или избыточной адсорбцией (Г).
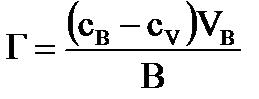 ,
,
где CB,CV- концентрации адсорбата в поверхностном слое и в объеме;
VB - объем раствора;
B - площадь поверхностного слоя.
Виды зависимости адсорбции от параметров системы
| а) изотермы | б) изопикны | в) изобары | г) изостеры |
| А=fT(c) A=fT(P) | A=fC(T) | А=fP(T) | c=fA(T) P=fA(T) |
| s= f(c) |
| С |
| Г s |
| Г= f(c) |
| a |
| Р и с. 2.2.2.1. Схема графического расчета изотермы адсорбции |
| a0 |
 - фундаментальное адсорбционное уравнение Гиббса
- фундаментальное адсорбционное уравнение Гиббса
Предположим, что g = 1 (при с ® 0). Тогда  - для жидкости и газа Зная зависимость
- для жидкости и газа Зная зависимость  = f( с ) (где с - концентрация растворенного вещества), можно рассчитать изотерму адсорбции, пользуясь адсорбционным уравнением Гиббса. Схема графического расчета показана на рис. 2.2.2.1: Тангенс угла наклона соответствует значениям производных
= f( с ) (где с - концентрация растворенного вещества), можно рассчитать изотерму адсорбции, пользуясь адсорбционным уравнением Гиббса. Схема графического расчета показана на рис. 2.2.2.1: Тангенс угла наклона соответствует значениям производных  в этих точках.
в этих точках.
Зная эти производныеуравнения Гиббса, можно рассчитатьзначение Г, что позволяет построить зависимость Г = f(С). Уравнение Гиббса показывает, что единица измерения гиббсовской адсорбции не зависит от единицы измерений концентрации, а зависит от размерности величины R. Так как величина R отнесена к молю вещества, а s- к единице площади, то Г = [моль/ единица площади]. Если s выразить в [Дж/м2], то R нужно подставлять: R= 8,314 Дж/моль×К.
В уравнении Гиббса влияние природы вещества на адсорбцию отражается производной  . Эта производная определяет и знак гиббсовской адсорбции, и может служить характеристикой вещества при адсорбции. Чтобы исключить влияние концентрации на производную берут ее предельные значения, т.е. при стремлении концентрации к нулю. Эту величину Ребиндер назвал поверхностной активностью.
. Эта производная определяет и знак гиббсовской адсорбции, и может служить характеристикой вещества при адсорбции. Чтобы исключить влияние концентрации на производную берут ее предельные значения, т.е. при стремлении концентрации к нулю. Эту величину Ребиндер назвал поверхностной активностью.
 ;
;
g = [Дж×м/моль] = [Н×м2/моль]; [эрг см/моль] = [Гиббс].
Уравнение показывает, что чем сильнее снижается  = f(c) с увеличением концентрации, тем больше поверхностная активность этого вещества.
= f(c) с увеличением концентрации, тем больше поверхностная активность этого вещества.
Физический смысл поверхностной активности состоит в том, что она представляет силу, удерживающую вещество на поверхности и отнесенную к единице гиббсовской адсорбции.
1.  2<
2<  1, тогда
1, тогда  <0 и Г>0: g>0 Þ с увеличением концентрации поверхностное натяжение на границе раздела фаз убывает и вещество поверхностно-активно.
<0 и Г>0: g>0 Þ с увеличением концентрации поверхностное натяжение на границе раздела фаз убывает и вещество поверхностно-активно.
2.  2>
2>  1, то g<0: Г <0 Þ вещество поверхностно-инактивно.
1, то g<0: Г <0 Þ вещество поверхностно-инактивно.
3. g = 0, Г = 0 - адсорбции нет, т.е. вещество индифферентно.
Поверхностно-активными веществами являются органические вещества, состоящие из углеводородного радикала и функциональной группы. Неорганические соли являются поверхностно-инактивными веществами. Ребиндер и Щукин в своих работах показали, что развитие микротрещин в твердых телах при деформации может происходить гораздо легче при адсорбции веществ из среды, в которой ведется деформирование: адсорбироваться могут как ионы электролитов, так и молекулы поверхностно-активного вещества (ПАВ), образуя на адсорбирующей поверхности их двумерный газ в результате нелокализованной адсорбции. Молекулы под давлением этого газа проникают в устье трещин и стремятся раздвинуть их, таким образом содействуя внешним силам, т.е. наблюдается адсорбционное понижение твердости твердого тела, что получило название эффекта Ребиндера. Поверхностная активность в гомологическом ряду поверхностно-активных веществ (ПАВ) повышается в среднем в 3,2 раза на каждую группу СН2 (в водных растворах) – правило Дюкло – Траубе. [2]
Существуют различные теории адсорбции.
Закон Генри - величина адсорбции при малых давлениях газа (малых концентрациях вещества в растворе) прямо пропорциональна давлению (концентрации). При адсорбции на твердых телах область действия закона мала из-за неоднородности поверхности, но даже на однородной поверхности при увеличении концентрации обнаруживается отклонение от закона. При малых концентрациях распределенного вещества отклонения обусловлены в основном соотношением между взаимодействием молекул друг с другом и с поверхностью адсорбента. Если когезионные взаимодействия адсорбата больше, то отклонение от закона отрицательно и g <1. Если сильнее взаимодействие «адсорбат – адсорбент», то отклонение положительно. При дальнейшем увеличении концентрации происходит уменьшение свободной поверхности, снижается реакционная способность и кривые загибаются к оси абсцисс.
Теория Ленгмюра позволяет учесть наиболее сильные отклонения от закона Генри. Положения теории:
1. Адсорбция локализована на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбента - образуется мономолекулярный слой.
2. Адсорбционные центры энергетически эквивалентны - поверхность адсорбента эквипотенциальна.
3. Адсорбированные молекулы не взаимодействуют друг с другом.
Ленгмюр предположил, что при адсорбции происходит квазихимическая реакция между распределяемым компонентом и адсорбционными центрами поверхности.
 - для жидкостей;
- для жидкостей;  - для газов.
- для газов.
Эти выражения – уравнения изотермы адсорбции Ленгмюра. К и Кр в уравнении характеризуют энергию взаимодействия адсорбента с адсорбатом.
Экспериментальные результаты по определению изотермы адсорбции обычно обрабатывают с помощью уравнения, записанного в линейной форме;
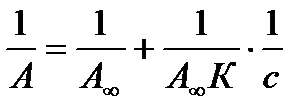 , т.е. уравнение типа y = b + ax.
, т.е. уравнение типа y = b + ax.
Такая линейная зависимость позволяет графически определить А¥ и К. Если сà 0, тогда уравнение примет вид:
А=А¥Кс;  ; А = Кгс, q =Кс,
; А = Кгс, q =Кс,
т.е. при сà 0 уравнение Ленгмюра переходит в уравнение Генри.
Если сà¥, тогда А = А¥, А/А¥ = 1. Это случай предельной адсорбции.
| Рис.2.3.1.3.Схема полимолекулярной адсорбции по теории БЭТ |
| А |
| p/ps |
| Р и с. 2.3.1.2. Изотерма полимолекулярной адсорбции |
 .
.
Прологарифмировав, получим  , где k, n – постоянные.
, где k, n – постоянные.
Использование уравнения Фрейндлиха в логарифмической форме позволяет определить константу уравнения.
Уравнение Ленгмюра можно использовать только при адсорбции в мономолекулярном слое. Это условие выполняется при хемосорбции, физической адсорбции газов при малом давлении и температуре выше критической. Однако в большинстве случаев мономолекулярный адсорбционный слой не компенсирует полностью избыточную поверхностную энергию и поэтому остается возможность влияния поверхностных сил на второй и т.д. адсорбционные слои. Это реализуется в том случае, когда газы и пары адсорбируются при температуре ниже критической, т.е. образуются полимолекулярные слои на поверхности адсорбента, что можно представить как вынужденную конденсацию.
В результате этих представлений была выведена следующая формула:

|

|
| a |
| Р и с. 2.3.1.4. Линейная форма изотермы адсорбции БЭТ |

|
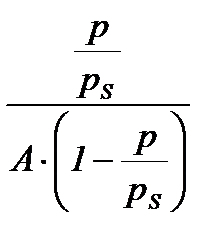
|
 - уравнение полимолекулярной адсорбции БЭТ,
- уравнение полимолекулярной адсорбции БЭТ,
где  ;
;
KL = aж/ап – константа конденсации пара;
аж - активность вещества в жидкости;
ап - активность вещества в состоянии насыщенного пара;
ап = рs.
Физический смысл С: характеризует разность энергии Гиббса в процессах чистой адсорбции и конденсации.
При р/рs<<1, уравнение БЭТ превращается в уравнение Легмюра, которое при дальнейшем уменьшении давления (pà 0) переходит в закон Генри:
 .
.
При обработке экспериментальных данных уравнение БЭТ используют в линейной форме (рис. 2.3.1.4):
 ;
; 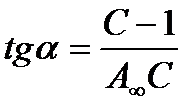 .
.
Таким образом графически находят обе константы уравнения А¥ и С.
В качестве твердых адсорбентов используют пористые тела.
По классификации М.М. Дубинина за основу принят размер пор и механизм протекающих на них процессов.
1. Макропористые тела. Радиус пор от 100 - 200 нм, Sуд = 0.5 - 2 м2/г - Для этих адсорбентов пригодна теория адсорбции Ленгмюра. В адсорбентах и катализаторах макропоры выступают в качестве транспортных каналов и адсорбцией в них можно пренебречь.
2. Переходно-пористые тела. Радиус пор более 2 - 100 нм, Sуд = 100 - 500 м2/г. Для них характерна полимолекулярная адсорбция, которая с увеличением давления заканчивается капиллярной конденсацией.
3. Микропористые тела. Радиус пор 0.5 - 2 нм, Sуд = 500 - 1000 м2/г. Отличительной особенностью этих тел является чрезвычайно близкое расположение противоположных стенок в порах. При этом их поля поверхностных сил перекрываются и они действуют во всем объеме микропор. К ним применима теория объемного заполнения микропор.
Реальные и промышленные адсорбенты имеют набор всех пор, но соотношение пор с разными радиусами различно. Каких пор больше, к такому классу их и относят.
Влияние структуры пористого тела на адсорбцию заметно проявляется уже на переходно-пористых телах. Это обусловлено проявлением капиллярных сил. Появление этого эффекта связано со сродством адсорбата к адсорбенту. Основываясь на закономерностях капиллярных явлений, можно утверждать, что сродство должно быть достаточно для смачивания поверхности твердого тела жидкостью, появляющейся в результате конденсации в порах. Только в случае смачивания адсорбент будет втягивать в поры адсорбат, увеличивая тем самым адсорбцию. Чем меньше размер пор, тем сильнее капиллярное удерживание адсорбата. Если поверхность не смачивается, то наблюдается явление капиллярного выталкивания, адсорбция в этом случае минимальна и возможна только в крупных порах. Адсорбция в переходно-пористых телах происходит по механизму капиллярной конденсации. Капиллярная конденсация начинает проявляться при определенной степени заполнения адсорбента или при определенном давлении пара, характерном для данной системы. К этому моменту поверхностная энергия адсорбции практически полностью скомпенсирована в результате полимолекулярной адсорбции, а макропоры заполнены адсорбатом. В результате повышения давления пара заполняются конденсатом все крупные поры. Размеры радиусов менисков подчиняются уравнению капиллярной конденсации Томсона (Кельвина).
 ,
,
где р - давление пара над искривленным мениском;
рs - давление насыщенного пара над плоской поверхностью;
s - поверхностное натяжение конденсированной жидкости;
r - радиус кривизны мениска.
При смачивании обеспечивается отрицательная кривизна мениска конденсата (вогнутый мениск), конденсация в порах наступает при давлении, которое меньше давления насыщенного пара, т.е. р/рs<1. Адсорбция является первым этапом капиллярной конденсации, если адсорбционные силы очень велики, а капилляры очень узкие, то конденсация идет до тех пор, пока не будет достигнуто давление насыщения над поверхностью.
| р/рs |
| А |
| Р и с. 2.3.2.1. Изотерма адсорбции при капиллярной конденсации: 1 – адсорбционная кривая; 2 – десорбционная кривая |
Пористые структуры разнообразны, однако считается, что их можно смоделировать тремя видами:
1) конусообразные;
2) цилиндрические с одним открытым концом;
3) цилиндрические с двумя открытыми концами.
В реальных адсорбентах имеются все виды пор, которые заполняются при разных давлениях, поэтому реальные изотермы имеют вид, представленный на рис. 2.3.2.2.
В первой группе в конусообразных порах конденсация начинается со дна пор, где кривизна наибольшая. По мере заполнения поры радиус мениска увеличивается (уменьшается кривизна), поэтому для дальнейшего заполнения поры необходимо увеличить давление (рис. 2.3.2.2, а). Процесс десорбции идет в обратном направлении и описывается той же кривой.
Во второй группе конденсация также начинается со дна, где кривизна сферическая и поэтому наибольшая (см. рис. 2.3.2.2, б). Так как пора цилиндрическая, то она заполняется целиком при определенном радиусе мениска, что отвечает и определенному давлению пара. Капиллярная конденсация в этих порах также происходит обратимо.
| Р и с. 2.3.2.2. Виды пор и соответствующие им изотермы адсорбции: а – конусообразная пора; б – цилиндрическая пора с одним открытым концом; в – цилиндрическая пора с двумя открытыми концами |
| р/рs |
| А |
| А |
| А |
| р/рs |
| р/рs |
| а |
| б |
| в |
В третьей группе (в): конденсация начинается на стенках пор, имеющих кривизну, в 2 раза меньшую сферы того же радиуса. Поэтому заполнение происходит при больших давлениях пара. Конденсация на стенках приводит к уменьшению радиуса пор и ее мгновенному заполнению при давлении, отвечающем началу конденсации. На концах образуются сферические мениски жидкости. Десорбция может начаться при давлении, соответствующем радиусу кривизны этих менисков. Таким образом, опорожнение происходит при меньшем давлении, чем ее заполнение. Это и объясняет наличие гистерезиса на изотерме адсорбции. В некоторых случаях гистерезис вызывается кинетическими факторами (смачивание).
Поиск по сайту: