Періодичні сигнали

З визначення періодичності випливає, що кожний сигнал (функція), що підходить під це визначення, ставиться до групи детермінованих сигналів. Якщо ця функція, крім того, задовольняє в межах одного періоду так називаним умовам Дірихле, тобто, по-перше, усюди однозначна, кінцева і кусочно-безупинна і, по-друге, має обмежене число максимумів і мінімумів, то її можна подати у вигляді безкінечної суми ортогональних функцій, тобто ортогонального ряду, що має вигляд

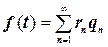, (4.3)

у який є множиною лінійно-незалежних функцій, тобто таких функцій, жодна з який не може бути виражена лінійною комбінацією інших функцій.

Для математично коректного здійснення розкладання коефіцієнти повинні вибиратися так, щоб виконувався критерій збіжності в середньому або середньому квадратичному, тобто

. (4.4)

Ця вимога для систем ортогональних або ортонормованних функцій виконується порівняно просто. Ортогональними іменуються функції, що виконують у потрібному для нас проміжку від t₁ до t₂ (протягом одного періоду) умову

, (4.5)

де n¹m. Включена у вираз (4.5) функція v(t) називається базової або вагової. Ортонормованними іменуються ті функції, що, крім умови (4.5), виконують також умову

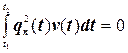. (4.6)

Легко переконатися, що основна тригонометрична система функцій 1, cos х:, sin x, cos 2x, sin 2х... ортогональна з ваговою функцією, рівна одиниці, але не ортонормованна.

Розрахунок коефіцієнтів Гц зводиться до такогоОбидвісторони вихідного рівняння (4.3) множаться на і v(t) і нтегруються в проміжку від t₁ до t₂,тобто

.

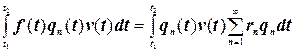У силу ортогональности функцій одержуємо

. (4.7)

Якщо система функцій ортонормована, те знаменник формули (4.7) дорівнює одиниці.

Одним із найбільше поширених засобів представлення детермінованих сигналів є ряд Фур’є:

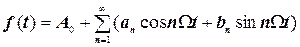. (4.8)

У цьому виразі A₀, a_n і b_n -незалежні від часу коефіцієнти, що варто розуміти як A₀ - середнє значення постійної складового сигналу (функції), а a_n і b_n - амплітуди членів розкладання, або гармонік. Перераховані коефіцієнти обчислюються по формулах

, (4.9)

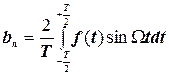, (4.10)

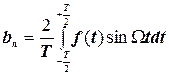, (4.11)

Приведеного виразу отримані шляхом множення обох сторін рівняння ряду Фур’є (4.8) на ту саму тригонометричну функцію (sin nWt, cos nWt) до інтеграції їх у межах періоду.

Якщо розглянута функція f(t) парна, тобто 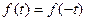, то b_n обертається в нуль; якщо непарна, тобто, , те a_n обертаються в нуль.

Представлення функції у вигляді ряду Фур’є єїї спектральним виразом, тому що розкриває частотний склад розглянутого сигналу. Спектр періодичної функції називається лінійчатим, або дискретним, тому що складається з окремих ліній, що відповідають дискретним частотам.

Крім приведеної форми запису ряду Фур’є (4.8) поширена також тригонометрична форма, що має перед раніше розглянутої деякої формально-математичної переваги. Вона має вид

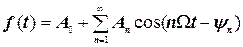. (4.12)

Її коефіцієнти виражаються через раніше обчислені [див. вирази (4.9) - (4.11)] шляхом нескладних перетворень. З огляду на те, що

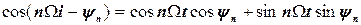
одержуємо

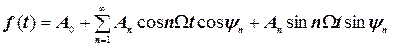
отже,

,

або

.

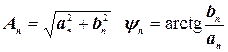У випадку такого подання сигналу коефіцієнт A_nіменується модулем амплітуди, а y_n - фазою відповідної гармоніки.

У ряді випадків вигідно користуватися комплексною модифікацією приведеного ряду (4.8). Її одержують, використовуючи перетворення формули Ейлера, тобто виразу

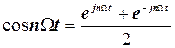, (4.15)

. (4.16)

Підставляючи ці вирази у формулу (4.8), одержуємо

,

або

.

Виходячи з того, що, відповідно до виразів (4.10) і (4.11),

і з огляду на рівності (4.15) і (4.16), цей вираз можна переписати у вигляді

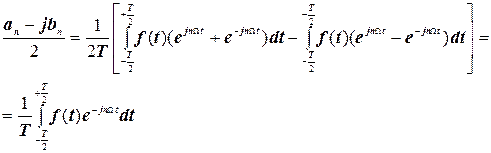
і аналогічно

.

А відповідно до виразу (4.9)

,

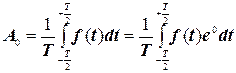то можливо формулу (4.17) записати у вигляді

, (4.18)

де

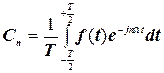(4.19)

є комплексною амплітудою n-й гармоніки для .

Формули (4.18) і (4.19) іменуються парою перетворень Фур’є. Друга з них дозволяє знайти спектр, тобто,сукупністьгармонійнихскладових, утворюючих у сумі вихідну функцію f(t). Перша дає можливість обчислити функцію, якщо відомі її гармонійні складові.

Комплексна амплітуда С_n пов’язана з раніше введеними коефіцієнтами в такий спосіб:

. (4.20)

Виражений формулою (4.18) спектр поширюється на значення n від -¥ до +¥, тобто як на позитивні, так і на відємні частоти. Звісно негативні частоти в природі не існують. У отриманому виразі вони мають чисто формальний, математичний характер, обумовлений застосуванням, комплексної форми запису для представлення реальної функції часу.

Однією із найважливіших властивостей періодичного сигналу є те, що повна потужність, що виділяється їм на якийсь навантаженні (заради спрощення розрахунку звичайно розглядається потужність, що виділяється на опорі в 1 Ом), є сумою середніх потужностей, що виділяються постійною складовою і кожною з гармонік сигналу окремо. Таким чином, по огибаючій гармонік можна судити про розподіл потужності в спектрі періодичного сигналу. Довести викладене можна, базуючись на тому, що розкладання функції в ряд Фур’є дає ряд ортогональних функцій. Так,

, (4.21)

де 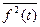означає усереднене в часі значення. Опір навантаження прийнято рівним 1 ом. Підставляючи у вираз (4.21) замість функції її розклад в ряд Фур’є (4.8), дістаєм

.

Отже, одержуємо суму інтегралів, що містять такі члени: 1) ;

2) ;

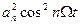3) ;

4) добутки косинусів і синусів, що мають аргументи неоднакової кратності. Ці останні при інтегруванні в межах періоду в силу умови ортогональности перетворюються в нуль. Таким чином, вираз (4.22) приймає вид

або

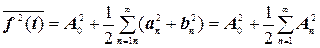. (4.23)

Поиск по сайту: