Структура оптимальних приймачів

Структуру оптимального приймача для прийому дискретних повідомлень за принципом максимальної зворотної ймовірності (рис. 8.2) характеризує наявність обчислювачів (корелятора), на які подаються прийняті й очікувані (можливі) сигнали. Одержувані в обчислювачах зворотні ймовірності кожного з можливих дискретних сигналів порівнюються на схемі порівняння СП. Остання, вибираючи максимальну зворотну ймовірність, вирішує, який

Рисунок 8.2 – Структура оптимального приймача.

з можливих сигналів сприйнятий. Значення можливих сигналів, що характеризуються їхніми апріорними ймовірностями й енергіями, грають у схемі оптимального приймача роль зсувів.

Найпростішим з можливих випадків прийому дискретних повідомлень є так назване бінарне виявлення. Воно відповідає випадку прийому бінарного коду – нуля чи одиниці, тобто

х₀(t)=0; x₁(t)=u_c(t). (8.33)

У цьому випадку зважується, чи мається на вході приймача сигнал u_c(t) (і шум) чи сигнал відсутній (тобто існує тільки шум). Структура приймача для бінарного виявлення істотно спрощується (рис 8.3), і він являє собою сполучення корелятора і пристрою, що порівнює, отримане значення з порогом (постійним негативним зсувом). Установлення названого порога залежить від обраного критерію.

Рисунок 8.3 – Структура приймача бінарного виявлення.

Для випадку бінарних сигналів критерій мінімальної середньоквадратичної помилки іменується також критерієм мінімальної повної ймовірності помилки чи критерієм ідеального спостерігача. Він зводиться до

Р_пом=Р(х₀)Р_пт+Р(х₁)Р_пр=min, (8.34)

Де х₀=0;

х₁=1;

Р_лт – ймовірність помилкової тривоги;

Р_пр – ймовірність пропуску.

У ряді випадків наслідки помилкової тривоги і пропуски можуть виявитися непорівнянними. У такому випадку доцільне застосування критерію мінімального середнього ризику R. Відповідно до цього критерію,

R=a(x₀)P_пт + b(x₁)P_пр =min, (8.35)

де a і b – вагові коефіцієнти, обрані з урахуванням відносної небезпеки помилкової тривоги і пропусків.

Для випадку, коли апріорні ймовірності надходження нулів і одиниць невідомі, може бути використаний критерій мінімальної зваженої імовірності помилки

Z= cP_пт + dP_пр =min, (8.36)

де с і d – вагові коефіцієнти.

Через те, що на практиці обґрунтований вибір вагових коефіцієнтів представляє істотні труднощі, він часто заміняється вибором припустимої імовірності помилкової тривоги, що приводить до так названого критерію Неймана-Пірсона, відповідно до якого

Р_пр=min;

Р_лт=const. (8.37)

Так як формули (8.34) і (8.35) можуть розглядатися як окремі випадки критерію мінімальної зваженої ймовірності (8.36), що може бути записано виразом

Z’=P_пр+ ßР_пт = min, (8.38)

де поріг ß=c/d, то для перших трьох критеріїв структура оптимального приймача виходить однакової, різними виявляються тільки значення порога ß. То ж може бути доведене і для критерію Неймана-Пірсона.

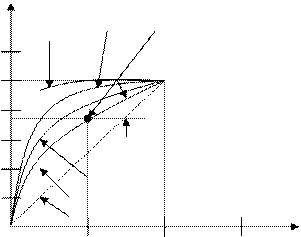
Основними характеристиками оптимального приймача є так названі робочі характеристики (рис. 8.4).

Р_ПО=1-Р_ПР

q=4 q=2 M(b)

1,2

1,0 Д(b=0)

0,8 y

0,6

0,4 q=1

0,2 q=0,5

q=0

0 Р_ПТ

0,5 1 1,5

Рисунок 8.4 – Робочі характеристики оптимального приймача.

Кожна з них дає залежність імовірності правильного виявлення Р_по від імовірності помилкової тривоги Р_пт при одному із заданих значень енергетичного відношення сигнал/шум q.

Розташування крайніх точок характеристик випливає з логічних закономірностей Р_по=0 при Р_пт=0 і Р_по=1 при Р_пт=1. Природно також, що при заданому значенні помилкової тривоги збільшення значення q веде до збільшення ймовірності правильного виявлення. Кожній точці М характеристики відповідає цілком визначене значення порога b. При зміні порога від нескінченності до нуля точка М переміщається по робочій характеристиці від початку координат у точку D. Для оптимальних, відповідно до перерахованих чотирьох критеріїв, приймачів виконується рівність

tg ψ = ß, (8.39)

де ψ – кут нахилу дотичної до робочої характеристики в заданій точці М. У випадку перших трьох критеріїв ß не залежить від значення відношення сигнал/шум q, у випадку ж критерію Неймана-Пірсона ß визначається по робочих характеристиках для заданих значень Р_пт і q і, отже залежить від значення відношення сигнал/шум.

Характеристики виявлення дають залежність імовірності помилкового виявлення від відношення сигнал/шум і дозволяють визначити мінімальний сигнал, що забезпечує задану якість виявлення. Для перших трьох критеріїв характеристики виявлення відповідно являють собою залежності Р_ош=f₁(q); R=f₂(q); Z=f₃(q), а для критерію Неймана-Пірсона Р_по=f4(q) при Р_пт= const. Для перших трьох критеріїв виявлення будуються в наступній послідовності. Спочатку розраховується поріг ß. Потім графічно визначаються відповідні йому точки на всіх робочих характеристиках (по одній на кожній). По відзначених точках для кожного q визначаються відповідні йому Р_пт і Р_пр, що дає можливість розрахувати відповідні Р_ош, R і Z. За знайденим значенням будується характеристика виявлення (рис. 8.5).

Рисунок 8.5 – Характеристика виявлення для критерія мінімальної повної ймовірності помилки.

Рисунок 8.6 – Характеристика виявлення для критерію Неймана-Пірсона.

Для критерію Неймана-Пірсона послідовність побудови характеристики виявлення зводиться до проведення вертикалі через точку (Р_пт, 0), де Р_пт - задана імовірність помилкової тривоги. Для кожної точки перетинання зазначеної вертикалі з робочою характеристикою визначаються значення Р_по і q. За цими значеннями будується шукана крива (рис. 8.6).

Поиск по сайту: