Оптимальні методи прийому

Забезпечення завадостійкості радіоприймача зводиться до відшукання найкращого способу прийому при наявності перешкод. Цим займається теорія оптимальних методів прийому, що застосовується при проектуванні радіопристроїв. Оптимальними методами прийому називаються такі методи, що забезпечують найкращий у тому чи іншому змісті прийом сигналів чи несучих ними повідомлень при наявності перешкод. Ті, що вкладається в поняття «найкращий», називається критерієм оптимальності. У такий спосіб перед тим як розглядати який-небудь метод прийому, варто чітко визначити критерій оптимальності прийому.

Одним з найбільш розповсюджених критеріїв оптимальності прийому є критерій максимального відношення сигнал/перешкода q_макс. Цей критерій виявляється цілком придатним для модульованих сигналів, тому що одержання на виході фільтра найбільшого відношення сигнал/перешкода в багатьох випадках забезпечує найбільш сприятливі умови для наступної демодуляції сигналу, тобто відтворення повідомлень. Для реалізації цього критерію необхідний приймач з оптимальним лінійним фільтром, що забезпечує максимальне відношення сигнал/шум, і з наступним демодулятором.

Передавальна функція К(W) оптимального лінійного фільтра (що забезпечує максимальне відношення сигнал/шум) може бути знайдена виходячи зі зворотного перетворення сигналу по Фур'є (4.27) і з виразу для флуктуаційної (самої інформативний) перешкоди, рівномірно розподіленої по всьому частотному діапазоні (7.13).

Розглядаючи відношення сигнал/шум на виході фільтра з передавальною функцією К(W) у момент часу t₀, що відповідає піку сигналу, одержуємо

. (8.28)

Відповідно до обраного критерію оптимальності, фільтр повинний мати таку передавальну функцію, щоб він забезпечував максимальне значення цього співвідношення. Екстремум виразу (8.28) визначається методом варіаційного числення і має місце при

(8.29)

що дає

q_макс=2Э/N₀, (8.30)

де Э – енергія сигналу на вході фільтра. Це позначає, що оптимальним у сенсі забезпечення максимального відношення пікового значення напруги сигналу до середньоквадратичного значення напруги шуму є такий лінійний фільтр, передавальна функція якого з точністю до постійного множника збігається зі спектральною характеристикою (амплітудним спектром) переданого сигналу. Величина q_макс не залежить від t₀, відповідно до формули (8.29).

Досліджуючи отриманий результат на предмет його фізичної реалізуємості, з'ясовуємо, що оптимальний фільтр здійснимо для усіх випадків, коли напруга на вході фільтра зникає до настання моменту, коли напруга на виході досягає максимуму. З огляду на це, одержуємо висновок, що оптимальний фільтр можливо реалізувати для багатьох, однак не для всіх реальних сигналів. Наприклад його не можна створити для сигналу, що загасає по експоненті.

Для сигналу, що має форму одиночного прямокутного імпульсу тривалістю t₀, спектральна характеристика виражається як

(8.31)

Вибираючи момент часу t₀=t₀, одержуємо передавальну функцію оптимального фільтра у виді

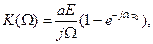(8.32)

реалізованому схемою, зображеної на рис. 8.1.

аЕ/jW РК

вхід вихід вихід

t

е^-jWt

Рисунок 8.1 – Блок-схема оптимального фільтра.

На схемі інтегруюча ланка IЛ з коефіцієнтом передачі аЕ/jW відповідає першому множнику формули (8.32), лінія затримки ЛЗ дає затримку на час t₀ і в комбінації з різницевим каскадом РК забезпечує коефіцієнт передачі (1-e^-jWt₀), що відповідає іншому множнику формули (8.32). У підсумку на виході фільтра виходить напруга трикутної форми. Таким чином, оптимальний фільтр перетворює прямокутний імпульс у трикутний подвоєній тривалості.

Поряд з оптимальними часто зустрічаються лінійні квазіоптимальні фільтри. Це фільтри, форма частотної характеристики яких задана заздалегідь, а максимальне значення відношення сигнал/шум досягається підбором ширини смуги пропущення цієї частотної характеристики.

Іншим часто вживаним критерієм оптимальності є критерій мінімальної середньоквадратичної помилки. Якщо в першому випадку, коли використовувався оптимальний фільтр, ставилася задача оптимального відтворення на тлі перешкод усього сигналу, то зараз ставитися задача оптимального відтворення повідомлення. У цьому випадку навіть дуже сильна зміна (перекручування) форми сигналу ще не свідчить про перекручування несеного ним повідомлення.

Критерій мінімальної середньоквадратичної помилки при великому відношенні сигнал/перешкода у випадку перешкоди, що має характер білого шуму, тобто рівномірно розподіленої по частотному діапазоні з гаусовим розподілом амплітуд, виконується приймачем, що діє за принципом максимальної зворотної імовірності. Останні поняття породжене припущенням, що жоден приймач у принципі не може відтворити повідомлення досконало точно і що у всіх випадках буде існувати деяка імовірність помилки. Тому від ідеального приймача потрібно, щоб він обчислював розподіл ймовірностей (чи густин ймовірностей) Р_у(х) усіх можливих значень прийнятого повідомлення. Розподіл Р_у(х) називається апостеріорним чи розподілом зворотних ймовірностей, тому що воно вказує, які імовірності значень «причини» x, якщо відомий викликаний цією причиною наслідок y.

На основі аналізу розподілу зворотних ймовірностей приймається рішення про те, яке було значення переданого повідомлення. Рішення може здійснюватися самим приймачем, якщо в нього закладене правило ухвалення рішення. Таким правилом може бути принцип максимальної зворотної імовірності, при дотриманні якого на виході приймача завжди виявляється найбільш ймовірне значення повідомлення.

Пристрій, що практично реалізує обчислення зворотної ймовірності повідомлення, називається корелятором, тому що він визначає взаємну кореляцію прийнятого й очікуваного повідомлення. Корелятор є основним елементом оптимального приймача. У якості такого може використовуватися також оптимальний лінійний фільтр.

Обчислення коефіцієнта кореляції для якогось одного конкретного значення повідомлення не представляє труднощів. Однак для визначення повідомлення, що має максимальну зворотну імовірність, коефіцієнт кореляції повинний бути знайдений для всіх можливих значень повідомлення, що набагато сутужніше. Труднощі істотно зменшуються у випадку дискретного повідомлення (що має кінцеве число можливих дискретних значень), причому структура приймача тим простіше, чим менша кількість можливих дискретних значень повідомлення.

Поиск по сайту: