Надійні інтервали для математичного сподівання та середнього квадратичного відхилення

Довірчі інтервали для оцінки математичного сподівання при відомому

Припускаючи, що випадкова величина Х розподілена нормально, причому середнє квадратичне відхилення цього розподілу відоме. Потрібно оцінити невідоме математичне сподівання по вибірковій середній x_В, тобто поставимо задачу знаходження довірчого інтервалу, що накриває параметр m з надійністю .

Так як величина є сума n незалежних однаково розподілених випадкових величин Х_і, то згідно центральної граничної теореми її закон розподілу близький до нормального. Параметри розподілу такі:

.

Вимагаємо, щоб виконувалась рівність:

,

де - задана надійність.

Як відомо , а замінивши Х на і на , отримаємо:

, (1)

де .

Знайшовши з останньої рівності , можна записати

.

Зауважимо, що ймовірність Р (надійність) задана, і рівна , тому маємо

.

Смисл одержаного співвідношення такий: з надійністю можна стверджувати, що довірчий інтервал накриває невідомий параметр m; точність оцінки .З класичної оцінки 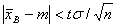випливає, що коли об’єм вибірки n зростає, то точність оцінки збільшується, а із збільшенням надійності збільшується t (Ф(t) – зростаюча функція), тобто зменшується точність.

Довірчі інтервали для математичного сподівання при невідомому

Нехай тепер випадкова величина Х генеральної сукупності розподілена нормально, але середнє квадратичне відхилення невідоме. Потрібно оцінити невідоме математичне сподівання з допомогою довірчих інтервалів, тобто задача пункту 1), але тепер невідоме.

Перш ніж розв’язувати цю задачу, введемо деякі поняття. Незалежні умови, що накладаються на n_i (чи W_i), називаються в’язами. Наприклад, - тобто вимога того, щоб співпадали теоретичні та вибіркові значення середнього арифметичного та дисперсії і т.д. Різниця між числом інтервалів та числом в’язей називається числом ступенів вільності k=n-r, де r – число в’язей.

Отже, користуючись розподілом Стьюдента, можна знайти довірчий інтервал:

, (2)

що накриває параметр m з надійністю . Тут та S шукається по вибірці, а по таблиці 3 (див. додаток) по заданих n можна знайти .

Довірчий інтервал для оцінки середнього квадратичного відхилення

Нехай випадкова величина Х генеральної сукупності розподілена нормально. Потрібно оцінити невідомий параметр – генеральне середнє квадратичне відхилення за “виправленим” вибірковим середнім відхиленням S_В. Поставимо перед собою задачу знаходження довірчого інтервалу, що накриває параметр , з заданою надійністю .

Вимагаємо виконання рівності , або .

Поиск по сайту: