АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Теорема множення ймовірностей незалежних подій

Читайте также:
  1. S-M-N-теорема, приклади її використання
  2. а) відношенню кількості елементарних подій, що сприяють події до кількості всіх
  3. Алгебра випадкових подій
  4. Б) Множення вектора на скаляр
  5. Блок множення Product
  6. Види подій
  7. Випадкові події. Класифікація подій
  8. Випишіть українські землі, що напередодні 1941 р. були приєднані до складу УРСР, зазначте, коли і внаслідок яких подій це сталося.
  9. Властивості ймовірностей подій
  10. Властивості щільності ймовірностей
  11. Внешние эффекты (экстерналии). Теорема Коуза.
  12. Внешние эффекты, их виды и последствия. Теорема Коуза

 

 

Якщо події А і В незалежні, то ймовірність добутку цих подій дорівнює добутку їх ймовірностей, тобто

(1)


Наслідок. Ймовірність добутку скінченої кількості незалежних подій дорівнює добутку ймовірностей цих подій

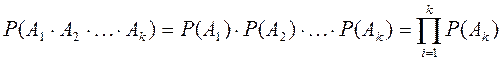
Задача 12. Студент шукає потрібну йому формулу у двох довідниках. Ймовірність того, що формула знаходиться у першому дорівнює 0,6, а у другому – 0,7. Знайти ймовірність того, що формула міститься в обох довідниках.

Розв’язання. Випробування – студент шукає формулу у двох довідниках.

Подія А1 – формула знаходиться у першому довіднику;

подія А2 – формула знаходиться у другому довіднику.

Оскільки існування формули в першому довіднику не залежить від ймовірності існування формули у другому довіднику і навпаки, то події А1, А2 – незалежні. Тому для розв’язання задачі скористаємося формулою (1) для випадку двох незалежних подій .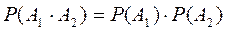

Маємо .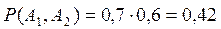

Відповідь: 0,42.

 



1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.)