АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Геометричне означення ймовірності

Читайте также:
  1. А) Означення множини. Операції над множинами
  2. Види умовних знаків топографічних карт, які видаються в Україні, пояснювальні підписи та цифрові позначення.
  3. Відносна частота. Статистичне означення ймовірності.
  4. Властивості ймовірності
  5. Геометричне визначення ймовірності
  6. Геометричне зображення комплексного числа. Модуль та аргумент комплексного числа
  7. Граничні теореми теорії ймовірності
  8. Задачі на класичну, статистичну і геометричну ймовірності
  9. Задачі на формулу повної ймовірності та формули Бейеса
  10. Ймовірність відхилення відносної частоти від сталої ймовірності в незалежних випробуваннях
  11. Класичне означення ймовірності

Щоб подолати недолік класичного означення ймовірності, яке полягає у тому, що його не можна застосувати до випробування з нескінченою кількістю елементарних подій, вводять геометричну ймовірність – ймовірність попадання точки в область.

Нехай 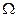– деяка область на прямій, площині або в просторі, а А – деяка частина області 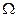. В області 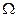навмання вибирають точку, вважаючи, що вибір точок області рівноможливий. Ймовірність того, що точка належить А, визначається рівністю

,

 

де – міра (довжина, площа, об’єм, час) А, .

Задача 11. На аудиокасеті записані концерти трьох співаків: першого – протягом 40 хв. звучання, другого – протягом 30 хв., третього – протягом 20 хв. Запис перемотується і навмання включається. Яка ймовірність того, що звучить пісня у виконанні другого співака?

Розв’язання Випробування – включається касета; подія А – звучить пісня у виконанні другого співака.

Час звучання запису Т()=90хв., час звучання другого співака Т(А)=30хв. За формулою (3) маємо .

Відповідь: .

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)