Рівень Б. 1. Кількість перестановок з n елементів по n обчислюють за формулою:

1. Кількість перестановок з n елементів по n обчислюють за формулою:

1) ;

2)

3)

2. Подія: усі студенти І курсу отримають диплом бакалавра є

1) достовірною;

2) випадковою;

3) неможливою.

3. Оберіть неправильне твердження:

1) сума двох протилежних подій – достовірна подія;

2) добуток двох протилежних подій – неможлива подія;

3) сприятливими для різниці подій А і В є елементарні події, які сприятливі і для А і для В.

4. Оберіть правильну тотожність:

1) ;

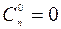2) ;

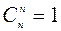3) .

5.Якщо елемент а можна вибрати із сукупності елементів m способами, а інший елемент b можна вибрати п способами, то вибрати а або b можна:

1) т+п способами;

2) т·п способами;

3) т–п способами.

6. Якщо події А і В незалежні, то ймовірність добутку цих подій дорівнює

1) добутку їх ймовірностей;

2) добутку ймовірностей однієї з них на умовну ймовірність іншої, за умови, що перша подія відбулася;

3) сумі їх ймовірностей.

7. Сума ймовірностей подій, що утворюють повну групу, не дорівнює:

1) нулю;

2) одиниці;

3) сумі їх ймовірностей.

8. Ймовірність настання принаймні однієї з подій А₁, А₂,..., А_п , незалежних в сукупності, знаходиться за формулою:

1) ;

2) ;

3) .

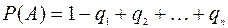9. Чи справедлива тотожність

1) так;

2) ні;

10. Аналітичний вираз має назву

1) формула Пуассона;

2) локальна теорема Муавра – Лапласа;

3) інтегральна теорема Муавра – Лапласа.

Поиск по сайту: