 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Індекси середніх величин. Якщо вивчається динаміка середніх величин, то використовують загальні індекси середніх величин
Якщо вивчається динаміка середніх величин, то використовують загальні індекси середніх величин.
Розглянемо їх на прикладі індексу середньої урожайності двох зернових культур: пшениці та гречки.
Як відомо, урожайність - це збір культури з одиниці площі: У = ВЗ/П, де ВЗ -валовий збір; П -розмір посівної площі. Тоді індивідуальний індекс урожайності, який характеризує динаміку урожайності окремої культури, обчислюється за формулою
iY = 
Загальний індекс характеризує динаміку середньої урожайності зернових

Цей індекс має назву індексу змінного складу; його величина залежить від двох факторів: зміни усередненого показника (в даному випадку врожайності) та зміни структури сукупності (співвідношення, питомої ваги площ під окремими культурами).
Для того щоб показати, як змінилась середня урожайність під впливом кожного фактора в окремості, обчислюють відповідно ще два індекси: індекс фіксованого складу та індекс впливу структурнихзрушень:

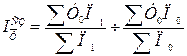
Очевидно, I 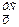 -можна записати у формі, що має назву агрегатної
-можна записати у формі, що має назву агрегатної
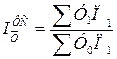
Якщо сам індекс показує зміну урожайності, То різниця між чисельником і знаменником його агрегатної форми показує зміну валового збору за рахунок зміни урожайності окремих культур.
Якщо на зміну середньої урожайності впливають два фактори, то на зміну валового збору — до того ж і третій — розмір посівної площі.
Приклад 7.3
Маємо дані про роботу двох шахт, які утворюють собою трест, за 1992 та 1993 pp. (табл. 7.3). Необхідно обчислити індивідуальні та загальні індекси продуктивності праці, загальний приріст видобутку вугілля та приріст за рахунок окремих факторів.
| Таблиця 7.3 | ||||||||
| № шахта | Видобуток вугілля, тисіт | Відпрацьовано людино-днів | Продуктивність праці т/л-дн | Частка у витрата, праці | ||||
| q0 | q1 | Т0 | Ті | We | Wi | d0 | di | |
| 2.0 | 2.2 | 0.4 | 0.67 | |||||
| 30.6 | ЗО | 1.5 | 1.53 | 0.6 | 0.33 | |||
| Разом | 118.6 | 1.7 | 1.997 | 1.0 | 1.00 |
Добудуємо таблицю та обчислимо підсумковий рядок. Продуктивність праці -- це видобуток вугілля за одиницю часу. Для шахти №1: Wt = 88000:40000 = 2,2 т/л-дн; W0 = 40000:20000 = 2,0 т/л-дн.
Отже, індивідуальний індекс продуктивності праці становить для шахти №1 — 1,1 (2,2/2,0), для шахти №2 - 1,02 (1,53/1,5) (табл. 7.4).
Таблиця 7.4 Таблиця розрахунків індексів середньої продуктивності праці
| № шахти | Iw | |
| 1,1 | ||
| 1,02 |
Таким чином, продуктивність праці у першій шахті зросла в 1,1 раза, або на 10%. Важливо підкреслити, що цей індекс ми називаємо і ндивідуальним, бо він відноситься до одиниці сукупності — шахти№1
Але зрозуміло, що вік, з іншого боку, характеризує зміну середньої продуктивності праці всіх шахтарів шахти №1, тобто сукупності. Аналогічно для другої шахти. Але якщо продуктивність праці на одній шахті зросла на 10%, а на другій - на 2%, то це зовсім не обов'язково, що в цілому по тресту вона зросла на 6%. Обчислимо загальний індекс продуктивності:
I 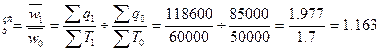 (116.3%)
(116.3%)
Виявляється, що продуктивність праці по тресту збільшилась на 16,3%, тобто ще в більшій мірі, ніж на кращій у цьому відношенні шахті.
Замість цього прикладу ми могли б запропонувати десятки інших. Хоч такий, в якому середня заробітна плата в колективі збільшилась у той час, коли одна! частина його в травні заробила тіж гроші, що в квітні, І а друга — навіть менші. На жаль завжди знайдуться такі, що не розуміють причин цього, що не зуміють правильно зрозуміти інформацію про середній рівень заробітної плати, споживання на душу населення, радіаційного забруднення тощо. Але інформацію про І зміну цих середніх, які хоч і є абстрактними, може [ торкнутись кожного з нас дуже конкретно.
Таким чином Iзс може виходити за межі індиві-| дуальних індексів. У нашому прикладі він показує І зміну середньої продуктивності за рахунок зміни продуктивності по кожній з шахт, а також за рахунок змін в структурі витрат часу.
Для того щоб визначити вплив першого фактору, обчислимо індекс фіксованого складу:
I 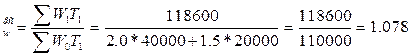
 (107,8%).
(107,8%).
На відміну від Iзс, IФС ніколи не виходить за межі індивідуальних індексів.
Поглянемо на табл. 7.3 з обчисленими даними. Легко помітити, що: продуктивність праці на першій шахті була вищою в кожному році; частка відпрацьованого на ній часу (а, як бачимо, використовується він більш ефективно, ніж на другій) різко збільшилась і стала більшою, ніж частка другої (67% проти 33%).
Ці зміни в структурі відпрацьованого часу позитивно позначились на зміні середньої продуктивності:
I 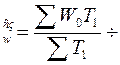

Тепер визначимо зміну видобутку вугілля по тресту — загальну і за рахунок окремих факторів:
 = 118600-85000 = 33600 т.
= 118600-85000 = 33600 т.
Фактори, які впливають на зміну загального видобутку вугілля, можуть бути різними, але в кінці кінців їх можна звести до двох: продуктивності праці та загальних витрат відпрацьованого часу:
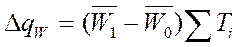 = (1,977 -1,7) • 60000 = 16600 т;
= (1,977 -1,7) • 60000 = 16600 т;
 = (60000 - 50000) • 1,7 = 17000 т.
= (60000 - 50000) • 1,7 = 17000 т.
Перевіримо:
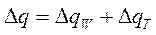 =6600 +17000 = 33600 т.
=6600 +17000 = 33600 т.
Поиск по сайту: