АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Особливості малої вибірки

Читайте также:
  1. Автоматизовані банки даних (АБД), їх особливості та структура.
  2. Банківська система: сутність, принципи побудови та функції. особливості побудови банківської системи в Україн
  3. В чому полягають особливості концепції особистості Ч.Кулі – 15 б.
  4. Валютні системи та валютна політика. особливості формування валютної системи України
  5. Види рядів динаміки та їх особливості
  6. ВИДИ ТЕКСТІВ ТА ОСОБЛИВОСТІ ЇХ РЕДАГУВАННЯ
  7. Види трудових договорів. Особливості окремих видів трудових договорів.
  8. Визначення необхідної чисельності вибірки.
  9. Визначте особливості концепції З. Фрейда – 15 б.
  10. Витоки російської та української філософської думки та особливості її становлення.
  11. ВІКОВІ ОСОБЛИВОСТІ ЕНДОКРИННОЇ СИСТЕМИ
  12. ВІКОВІ ОСОБЛИВОСТІ СЕНСОРНИХ СИСТЕМ

Малою вибіркою прийнято вважати вибірку, об'єм якої варіює в межах від 5 до 30 одиниць. Мала вибірка являється єдиним методом дослідження в тих випадках, коли організація суцільного або великого вибіркового спостережень неможлива. Переважно ви­бірковим методом користуються у випадку дослід­ження якості промислової продукції, при встановленні норм виробітку. Однак, слід відмітити, що необхідно бути обережним при використанні малої вибірки.

Як відомо з теорії вибіркового спостереження, ре­презентативність вибірки в значній мірі залежить від її обсягу. Випадкові помилки вибірки при достатньо ве­ликому обсязі розподіляються нормально. При цьому Допускається умова рівності генеральної та вибіркової Дисперсії.

За умови малої вибірки цим припущенням кори­стуватись не можна, її особливість якраз і полягає в тому, що випадкові помилки малої вибірки не підчиняються закону нормального розподілу. Тому для оцінки результатів малої вибірки і можливих границь її випадкової помилки користуються відношення^ Стьюдента:

де — стандартна помилка малої вибірки, яка обчис­люється за формулою

Як бачимо з цієї формули, в знаменнику береться не п, як у звичайній вибірці, а п-1, що являється принципово важливим у випадку для розрахунку помилки малої вибірки. Гранична ж помилка малої вибірки обчислюється стандартним способом за формулою

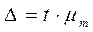
де t — це відношення Стьюдента.

Величина t підпорядковується закону розподілу Стьюдента (t вірне тільки для виборок, які взяті із генеральної сукупності з нормальним розподілом ознак). Для визначення ймовірності інтенсивності P(t) користуються спеціальними таблицями, в яких роз­раховані P(t) для даних значень t і k=n-1 (k - число ступенів вільності).

Наведемо приклад у вигляді табл. 4.5.

Таблиця 4.5

Імовірність P(t) розподілу t (Pk(t) • 1000)

t k
                ∞
2.0                  
2.5                  
3.0                  

 

За цією таблицею визначається двосторонній критерій, тобто імовірність того, що фактичне зна­чення t через випадкові причини не буде більшим від табличного за абсолютною величиною.

 

 

Приклад 4.7 [9]

На електроламповому заводі з метою перевірки якості ламп була організована мала вибірка (табл. 4.6). У випадковому безповторному відборі було відібрано 10 ламп.

Необхідно визначити граничну помилку вибірки і побудувати довірчий інтервал для середньої.

Таблиця 4.6

Розрахунок граничної помилки вибірки

 

Тривалість горіння, год (xi) Число ламп, шт. (fi)
           
           
           
           
Разом     х х  

 

Вибіркова середня дорівнює

год.,

вибіркова дисперсія:

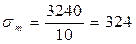
стандартна помилка:

год.

В умовах малої вибірки при k = п-1 =9 и t= 2,5 з імовірністю Pk(t), що дорівнює 0,966, гранична помилка за абсолютною величиною не перевищить

Λm= 2,5*6 = 15 год.

Імовірність того, що це твердження невірне і по­милка може вийти за встановлені межі 15 год., до­рівнює: 1 - 0,966 = 0,034.

На основі розрахованих характеристик будуємо до­вірчий інтервал для генеральної середньої:

1491 1521.

Питання для самоконтролю.

1. Для чого при проведенні вибіркового спостереження визна- 1 чається необхідний обсяг вибірки?

2. Чим визначається гранична помилка вибірки?

3. Що являє собою механічний спосіб відбору? Наведіть при- ' клад.

4. Які існують схеми відбору, умови їх застосування?

5. В чому полягають особливості типового відбору? Наведіть приклад.

6. Як перевірити репрезентативність вибіркової сукупності?

7. Як зміниться величина випадкової помилки, якщо обсяг ви­бірки збільшити на 21%?

8. Чи зміниться середня помилка вибірки, якщо замість повтор­ного відбору провести безповторний відбір?

9. За вибірковими даними питома вага бракованої продукції на першому підприємстві становить 3%, на другому — 5%. Для якого з них помилка вибірки буде більша і на скільки, якшо обсяг вибірки був однаковим?

10. Середня помилка вибірки для частки бракованої продукції становить 2%, питома вага браку у вибірці — 3%. З якою імовірністю можна стверджувати, що частка браку в гене­ральній сукупності не буде перевищувати 7%?

11. На ділянці лісу площею 1000 га необхідно визначити загаль­ний запас деревини (в куб. м). Випробувана площа становить 0,1 га. В результаті обстеження виявлено, що вихід деревини з 0,1 га становить 10 м3. Яким повинен бути обсяг вибірки, щоб помилка не перевищувала 4 м3 (р = 0,954)?

12. На поштовому відділенні міста планується проведення ви­біркового випадкового спостереження для визначення частки листів, адресованих за межі України. Результати необхідно оцінити з точністю!%(/> = 0,954). Скільки листів треба відібрати?

13. На підприємстві налічується 100 бригад однакової чисель­ності. Безповторно відібрано 36 бригад. За результатами ви­бірки середній стаж робітника становить 7 років. Міжсерійна дисперсія дорівнює 9 років. Визначити граничну помилку ви­бірки (р = 0,954).

14. В чому полягає особливість застосування малої вибірки?

15. Яким правилом користуються при визначенні граничної по­милки малої вибірки?

 

ТЕМА 5 Статистичні методи вимірювання взаємозв'язків.

ПЛАН ЛЕКЦІЇ

5.1. Види взаємозв 'язків між явищами.

5.2. Метод аналітичного групування. Дисперсійний аналіз.

5.3. Кореляційно-регресійний аналіз.

5.4. Багатофакторна кореляція.

5.5. Непараметричні методи вивчення взаємозв 'язків між явищами.

5.6. Рангова кореляція.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)