 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Види взаємозв 'язків між явищами
Всі явища та процеси, що існують в природі та суспільстві, взаємопов'язані, тому вивчення взаємозв'язків та причинних залежностей є одним із найважливіших завдань статистики. Причинна залежність є головною формою закономірних зв'язків, проте причина сама по собі ще не визначає повною мірою наслідок; останній залежить також від умов, у яких діє причина. Умови і причини являють собою фактори. Ознака, що характеризує наслідок, називається результативною, а та, що характеризує фактор, факторною.
Зв'язки між явищами поділяють на функціональні та стохастичні. При функціональному зв'язку кожному можливому значенню факторної ознаки х відповідає чітко визначене значення результативної ознаки у. Таку залежність ми маємо, наприклад, у фізичних, хімічних процесах та ін. Графічно вона має такий вигляд (рис. 5.1).

Рис. 5.1. Схематичне зображення функціонального зв'язку. У суспільних процесах - це переважно зв'язок між елементами розрахункових формул, наприклад, залежність валового збору від урожайності та посівної площі.
При стохастичном у зв'язку кожному значенню ознаки х відповідає певна множина ознаки у, які варіюють і утворюють ряд розподілу, який називається умовним. Стохастичний зв'язок проявляється зміною умовних розподілів. Графічно її можна представити на (рис. 5.2).

Рис. 5.2. Схематичне зображення стохастичного зв'язку.
Прикладом такого зв'язку можна навести залежність між рівнем кваліфікації та продуктивністю праці або залежність між кольором очей та кольором волосся.
Різновидом стохастичного зв'язку є кореляційний зв'язок, коли зі зміною факторної ознаки і змінюється середнє значення результативної ознаки.
5.2. Метод аналітичного групування. Дисперсійний аналіз.
У загальних рисах про метод аналітичних групувань вже йшлося в лекції 2, пункті 3. Він полягає в тому, що всі елементи сукупності групують за факторною ознакою і в кожній групі обчислюють середні значення результативної ознаки.
Проте було зазначено, що коли, наприклад, ми виділили групи робітників за розрядом, для кожної з яких обчислили середню заробітну плату, і побачили, що групам з більшим рівнем кваліфікації відповідає і більша середня місячна платня, то це нам дало підставу припустити, що між цими двома факторами («фах» -- «заробіток») є прямий зв'язок. Припустити, але не стверджувати. Стверджувати, зрозуміло з певною імовірністю, ми зможемо лише тоді, коли доведемо невипадковість, істотність відмінності (різниці) середніх, а тим самим істотність зв'язку. Це можна зробити, наприклад, за допомогою критерію Стьюдента. Таким чином можна визначити наявність зв'язку та його напрям.
Але на середній заробіток робітників певного розряду, крім фаху, впливають і інші фактори: захворюваність робітників, характер продукції, вік, стать та ін. Визначити внесок кожного з факторів, а також тісноту зв'язку дозволяє метод дисперсійного аналізу, суть якого розглянемо на такому прикладі (табл. 5.1).
Приклад 5.1
Маємо такі дані про годинний виробіток деталей робітниками двох груп, які пройшли перепідготовку (N1) і не пройшли (N2), чисельністю 5 чол. кожна.
Таблиця 5.7
Годинний виробіток робітників, які пройшли і не пройшли перепідготовку
| №п/п | Годинний виробіток деталей, Од. | Індивідуальне відхилення від загальної середньої | Квадрат індивідуального відхилення | |||
| група 1 | група 2 | група1 | група 2 | група 1 | група 2 | |
| -14 | ||||||
| -6 | ||||||
| -11 | ||||||
| -9 | ||||||
| -10 | ||||||
| Разом | -50 |
Дисперсійний аналіз дає можливість визначити роль систематичної та випадкової варіації у загальній варіації і тим самим визначити роль фактора, покладеного в основу групування, в зміні результативної ознаки. Для цього використовують правило складання дисперсії, згідно з яким загальна дисперсія дорівнює сумі двох дисперсій: середньої із групових і міжгрупової:


σ2заг.=δ 2 + 
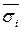
Тісноту зв'язку характеризує співставлення міжгру-пової дисперсії із загальною. Це відношення називається кореляційним відношенням:
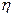 2 =
2 = 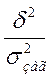
Обчислимо ці параметри для наведеного прикладу. Спочатку обчислимо групові та загальні середні.
Графи 4—7 табл. 5.1 є розрахунковими.
Загальна дисперсія, яка характеризує загальну варіацію під впливом усіх факторів, дорівнює
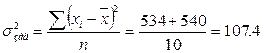
Загальна середня дорівнює
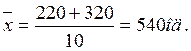
Міжгрупова дисперсія, яка характеризує факторну варіацію, тобто відмінності у виробітку, обумовлені тим, що частина робітників пройшла перепідготовку, становить:
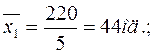

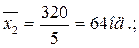
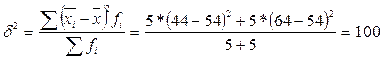
де fi- число одиниць у групі, i- число груп. Таким чином, кореляційне відношення становить
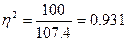 (тобто 93,1%)
(тобто 93,1%)
Це треба розуміти так, що 93,1 % всієї варіації обумовлено фактором, який покладено в основу групування, і тільки 6,9 % варіації є результатом дії інших. Такими, наприклад, можуть бути вік робітника, його стать та ін.
Кореляційне відношення змінюється від 0 до 1. Коли міжгрупова дисперсія дорівнює нулю, що можливо лише тоді, коли всі групові середні однакові, тобто коли кореляційний зв'язок між середніми відсутній. Причому міжгрупова дисперсія дорівнює загальній, а середня з групових -• нулю. Це означає, що кожному значенню факторної ознаки відповідає єдине значення результативної ознаки, тобто зв'язок між ознаками функціональний.
Припустимо, що ми поділили робітників на дві групи за ознакою числа літер у прізвищі (парне чи непарне) і обчислені групові середні відрізняються. Але в цьому випадку різниця є випадковістю.
Перевірку істотності (невипадковості) відхилень групових середніх здійснюють за допомогою статистичних критеріїв. У даному випадку можна використати критерій Фішера, або порівняти фактичне значення  з критичним (табличним).
з критичним (табличним).
У таблиці розподіл залежить від числа ступенів вільності факторної К1 та випадкової К2 дисперсій:.
К1 = m — 1, К2 = n— m;
де m - число груп;
n - загальний обсяг сукупності.
«Входами» в таблицю критичних значень є числа ступенів вільності К1,К2 та рівень значимості 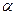 , який задається дослідником і характеризує, в якій мірі він ризикує помилитися в своєму припущенні (про «невипадковість»).
, який задається дослідником і характеризує, в якій мірі він ризикує помилитися в своєму припущенні (про «невипадковість»).
Для нашого прикладу
К1=2- 1 = 1, К2 = 10 - 2 = 8,
А 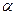 обернимо на рівні 5 %.
обернимо на рівні 5 %.
За таблицею критичних значень (див. додаток 1) для рівня істотності 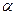 = 0,05 знаходимо
= 0,05 знаходимо 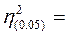 0,399.
0,399.
Це означає, що тільки в 5 випадках із 100 може випадково виникнути кореляційне відношення, яке перевищує значення 0,399. Тепер треба порівняти фактичне значення з критичним. Якщо воно більше критичного, то зв'язок між факторною і результативною ознакою вважається істотним:
0,931 > 0,399 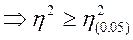 .
.
Тобто, зв'язок між фактом проходження робітником перепідготовки та зростанням продуктивності праці слід вважати істотним. При перевірці істотності зв'язку частіше використовують F-критерій Фішера, тому що при великих значеннях ступенів вільності його табличні значення мало змінюються, а таблиці менш громіздкі. За прикладами використання F-критерію при дисперсійному аналізі посилаємо до літератури [14, 17] (також див. додаток 2).
Як бачимо, при дисперсійному аналізі факторна ознака може бути як кількісною, так і якісною. Маючи названі переваги порівняно з методом аналітичних групувань, дисперсійний аналіз не дає змоги вивчити форму зв'язку.
Якщо ми маємо достатню кількість груп і кількісну факторну ознаку, то, довівши істотність зв'язку, можемо на координатах X та Y знайти певні точки, об'єднати їх ламаною і отримати певну модель форми зв'язку.
Поиск по сайту: