Кореляційно-регресійний аналіз

Головною характеристикою кореляційного зв'язку є лінія регресії. Лінія регресії х на у - це функція, яка зв'язує середні значення ознаки у зі зна­ченнями ознаки х. Залежно від форми лінії регресії розрізняють лінійний і нелінійний зв'язки. Лінія рег­ресії може бути представлена таблично, графічно, ана­літичне. У кореляційно-регресійному аналізі (КРА) оцінка лінії регресії здійснюється не в окремих точках, як в аналітичному групуванні, а в кожній точці інтервалу зміни фактичної ознаки х. Лінія регресії при цьому безперервна і зображується у вигляді певної функції Y = f(x), яка зветься рівнянням регресії, a Y -це теоретичні значення результативної ознаки.

Пояснимо суть КРА на простому прикладі (всі чи­слові значення умовні). Якщо ми знаємо, що відрізок металевої рейки певного правильного профілю дов­жиною 1 м важить 10 кг, то можемо назвати точну вагу, а точніше, масу будь-якого відрізку того ж профілю. Якщо ж ми маємо кілька відрізків, тобто стати­стичну сукупність, то можемо виміряти довжину кож­ного відрізка і обчислити його масу за формулою у = mх, де m -- маса відрізку довжиною 1 метр; х — довжина відрізку в метрах. Якщо нанести на графік точки з відповідними для кожного відрізка рейки ко­ординатами, то вони будуть знаходитися на одній прямій — зв'язок функціональний, лінійний (рис. 5.3).

Рис. 5.3. Точки графіка залежності маси рейки від її довжини.

Візьмемо другу сукупність — велику групу чоловіків у віці 20—45 років, про яких можна сказати, що вони мають звичайну, нормальну фігуру, тобто не дуже низькі або високі; товсті або худі (тобто являють со­бою однорідну сукупність). Тепер знайдемо для кож­ного з них відповідну точку в системі координат «зріст - маса»

Якщо при збільшенні чисельності сукупності рейок на рис. 5.3 все виразніше буде вимальовуватись пряма лінія з'являється так зване «кореля­ційне поле» — щось витягнуте, схоже на еліпс. При цьому цілком очевидно, що для певного значення оз­наки «зріст» (назвемо її факторною), скажімо в 180 см відповідає множина значень результативної ознаки «Маса»..

Виявилось, що всі хлопці, які мають однаковий зріст (наприклад, 180 см), мають різну масу, в нашому прикладі від 65 кг до 95 кг, або десь 80 ± 15 кг; можна і доцільно вести мову про середнє значення їх маси. Тут ми маємо умовний розподіл результатив­ної ознаки «маса». Він, як і будь-який ряд розподілу кількісної ознаки, характеризується параметрами та ін. Деякі з них ми вже визначили візуально, інші можемо обчислити. Припустимо: х = 80 кг; а = 5 кг.

Цікаво відмітити, що коли компанія хлопців буде досить великою, то їх розподіл за масою буде близь­ким до нормального. В природі масових явищ нор­мальний розподіл дуже поширений. Багато прикладів можна навести з біології, коли мова йдеться про нор­му, а не патологію. Нормально розвинені люди, на­приклад, нормально розподілені за зростом, масою, артеріальним тиском, життєвим об'ємом легень і т. д. Навпаки, в соціально-економічних явищах нормаль­ний розподіл зусрічається значно рідше. Можна уяви­ти собі розподіл населення України за рівнем доходів, який має довгий «правий хвіст». Слід пам'ятати, що від форми розподілу залежить вибір методів стати­стичного аналізу, особливо коли йдеться про пере­вірку гіпотез та вивчення зв'язку. Але повернемось до нашого прикладу і зробимо наступний висновок.

Між ознаками «зріст — маса» існує статистичний, кореляційний прямий зв'язок: при збільшенні зна­чення результативної ознаки «зріст» зростає середнє імовірне значення ознаки «маса». Таким чином, за­даючи конкретне значення фактора, ми можемо ви­значити імовірне значення результата.

Якщо кореляційне поле досить витягнуте, його можна уявити і змоделювати у вигляді певної функції, в нашому прикладі лінійного рівняння (рівняння рег­ресії):

Y=f(x),

де У— теоретичні значення результативної ознаки.

Тепер спробуємо собі уявити кореляційне поле, якщо раптом ми розглядаємо взаємозв'язок між озна­ками «зріст—поверх». Мабуть, воно буде подібне до того, що зображене на рис. 5.5. Неважко дійти вис­новку: при відсутності зв'язку між ознаками кореля­ційне поле не має певної форми. По мірі зростання тісноти зв'язку окремі точки стягуються ближче до деякої уявної лінії — лінії регресії (див.рис.5.4)

Рис. 5.5. Кореляційне поле прикладу «зріст—поверх».

Кореляційно-регресійний аналіз складається із та­ких етапів:

• вибір форми регресії;

• визначення параметрів рівняння;

• оцінка тісноти зв'язку;

• перевірка істотності зв'язку.

При виборі функції використовують графіки, аналітичні групування, теоретичне обгрунтування. Мож­ливий перебір функцій, коли обчислюють рівняння регресії різних видів і з них вибирають найкраще.

Найбільш поширена у статистичному аналізі ліній­на функція

Y = a+bx.

Параметр b називають коефіцієнтом регресії. Він показує, на скільки одиниць власного виміру в серед­ньому змінюється значення ознаки Y при збільшенні значення ознаки х на одиницю.Параметр а — це зна­чення Y при х = 0.

Якщо х не може приймати нульового значення, то а економічно не інтерпретується і як вільний член рівняння регресії має тільки розрахункове значення.

Ми пропонуємо читачеві, спираючись на свій жит­тєвий досвід, певні реальні значення параметрів для рівняння залежності маси людини від зросту. Іноді суть явища, яке вивчається, приводить до необхідності використання нелінійних рівнянь регресії. При цьому переважно використовують степеневу функцію:

Y = ax^b; або гіперболу Y = a+b/x

Визначення параметрів рівняння регресії прово­диться методом найменших квадратів, основною умо­вою якого є мінімізація суми квадратів відхилень ем­піричних значень від теоретичних; це дає можливість _; отримати найкращі оцінки параметрів а і Ь:

Для їх обчислення складають,і розв'язують систему нормальних рівнянь:

na+b

a

Для рішення системи використовують метод де­термінантів:

a=

b=

Визначення тісноти зв'язку в КРА, як і в методі дисперсійного аналізу, грунтується на правилі скла­дання дисперсій, але якщо оцінками лінії регресії в першому методі були значення середніх групових, ре­зультативної ознаки, то в КРА - теоретичні значення останньої. Дисперcію теоретичних значень називають факторною і обчислюють за формулою

Вона характеризує варіацію результативної ознаки, пов'язану з варіацією факторної ознаки. Замість се­редньої з групових дисперсій обчислюють залишкову, випадкову дисперсію:

Тоді загальна дисперсія розраховується за форму­лою

або

І де у_i — фактичне значення результативної ознаки; Y_i -теоретичне значення результативної ознаки; n - кількість рівней.

Вона характеризує варіацію результативної ознаки, не пов'язану з варіацією факторної ознаки. Мірою тісноти зв'язку в КРА є коефіцієнт детермінації, ана­логічний кореляційному відношенню:

R²⁼

де R² — коефіцієнт детермінатдії, — загальна дисперсія, факторна дисперсія.

Він приймає значення від 0 (при відсутності лі­нійного зв'язку) до 1 (зв'язок між ознаками функціональний). Тіснота зв'язку характеризує також ін­декс кореляції:

R =

Коли зв'язок між ознаками лінійний, використову­ють лінійний коефіцієнт кореляції, який, приймаючи значення від —1 до +1, характеризує не тільки тісноту зв'язку, а і його напрям. Його абсолютна величина збігається з індексом кореляції.

Його розраховують за наступною формулою:

_{r =}

Перевірку істотності зв'язку в КРА здійснюють за допомогою F-критерія Фішера:

F_R =

де m — число параметрів рівняння регресії.

Залежність між собівартістю одиниці продукції та обсягом її виробництва може приблизно бути пред­ставлена рівнянням двочленної гіперболічної регресії

виду Y = a+b/x Вона відрізняється від лінійної тількитим, що замість величини х там присутня 1/х. Тоді система нормальних рівнянь буде мати вигляд:

na+b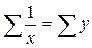

a

Для розв'язання цієї системи також використову­ють метод детермінантів:

a=

b =

Для розрахунку параметрів рівняння регресії, яка має форму степеневої функції, потрібно привести цю функцію до лінійного виду шляхом логарифмування:

lgF = lga + b1gx.

Отримане рівняння відрізняється від рівняння зви­чайної лінійної регресії тим, що замість Y, х, а існують їхні логарифми.

Приклад 5.2

За допомогою методу КРА визначити наявність та характер статистичного зв'язку між ознаками «вік ус­таткування» та «витрати на ремонт». Вихідні дані та проміжні розрахунки наведені в табл. 5.2 [18].

За даними таблиці можна обчислити і параметри рівняння. Отже, в нашому прикладі

а = (27 - 536 - 217,1 • 70)/(10 • 536 - 70 • 70) = -1,576;

b= (10 • 217,1 - 70 • 27)/(10 • 536 - 70 • 70) = 0.611.

Таким чином, зв'язок між віком устаткування та витратами на ремонт прямий. Лінійне рівняння регре­сії буде мати такий вигляд

Y=-1,576+ 0,611 х

Спочатку розрахуємо теоретичні значення Y (див. табл. 5.2, гр. 6), підставивши значення xу рівняння регресії.

Таблиця 5.2

Вік устаткування та витрати на ремонт для групи підприємств (умовні одиниці)

№ n/n	Вік устат­кування, р.(х)	Витрати на ремонт, тис. грн. (у)	x	ху	У	(уі-Уі)2
							8
		1,5		6,0	0,868	0,399	1,44
		2,0		10,0	1,479	0,271	0,490
		1,4		7,0	1,479	0,006	1,69
		2,3		13,8	2,09	0,044	0,16
		2,7		21,6	3,312	0,374	0,0
		4,0		40,0	3,312	0,285	1,69
		2,3		18,4	4,534	1,024	0,16
		2,5		17,5	2,7	0,04	0,04
		6,6		72,6	5,145	2,117	15,21
		1,7		10,2	2,09	0,152	1,0
Разом				217,1	27,01	4,712	21,92

Залишкова дисперсія дорівнює

;

Загальна дисперсія дорівнює

Тоді факторна дисперсія розраховується на підставі правила складання дисперсій

Коефіцієнт детермінації буде дорівнювати

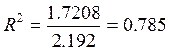
(або 78,5% загальної варіації витрат на ремонт зале­жить від варіації віку устаткування).

Обчислимо коефіцієнт кореляції за формулою

Це означає, що між віком устаткування та витра­тами на ремонт існує досить тісний прямий зв'язок.

Для перевірки істотності коефіцієнта кореляції за­стосовують спеціальну таблицю критичних значень. Величина п має значення на дві одиниці менше, ніж число спостережень. У нашому прикладі п = 10—2 = 8. Коефіцієнт буде істотним, якщо він перевищить відповідне табличне значення. Перевіримо істотність коефіцієнта кореляції за допомогою F-критерію:

При а =0,01 F(8,1) = 11,26. Це менше ніж фак­тичне значення (54,6).

Таким чином обчислений нами коефіцієнт коре­ляції є істотним і відображає тісноту зв'язку між віком устаткування та витратами на ремонт.

Можна скористуватись також і таблицею критич­них значень для t -критерію. Ступені вільності зале­жать від числа параметрів рівняння регресії m.

Поиск по сайту: